Identificazione del modello: adattamento dei modelli ai dati

Inizializzazioni

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from scipy.integrate import odeint
from scipy.optimize import minimize

Lettura dei dati

La cella seguente legge i dati di risposta al gradino sperimentali precedentemente memorizzati.

df = pd.read_csv("tclab-data.csv")
t = np.array(df["Time"])
T1 = np.array(df["T1"])
T2 = np.array(df["T2"])
Q1 = np.array(df["Q1"])
Q2 = np.array(df["Q2"])

Funzione di tracciamento

La seguente semplice funzione di tracciamento dei dati viene utilizzata in questo notebook per confrontare i dati sperimentali con le previsioni del modello.

def plot_data(t, T, T_pred, Q):
    
    fig = plt.figure(figsize=(8,5))
    grid = plt.GridSpec(4, 1)
    ax = [fig.add_subplot(grid[:2]), fig.add_subplot(grid[2]), fig.add_subplot(grid[3])]

    ax[0].plot(t, T, t, T_pred)
    ax[0].set_ylabel("deg C")
    ax[0].legend(["T", "T_pred"])
    
    ax[1].plot(t, T_pred - T)
    ax[1].set_ylabel("deg C")
    ax[1].legend(["T_pred - "])
    
    ax[2].plot(t, Q)
    ax[2].set_ylabel("%")
    ax[2].legend(["Q"])
    
    for a in ax: a.grid(True)
    ax[-1].set_xlabel("time / seconds")
    plt.tight_layout()
    
plot_data(t, T1, T1, Q1)
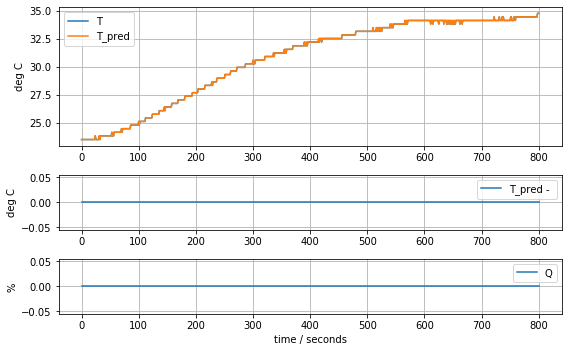
plot_data(t, T2, T2, Q2)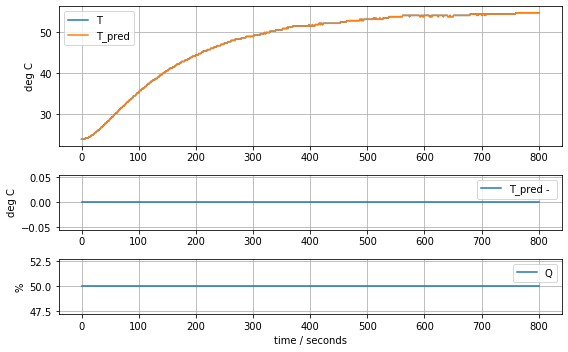

Modelli empirici

La modellazione empirica è un processo in cui tentiamo di scoprire modelli che descrivono accuratamente il comportamento input-output di un processo senza tener conto dei meccanismi sottostanti.

Modello lineare del primo ordine

Una funzione di trasferimento del primo ordine è modellata dall’equazione differenziale

\[ \tau \frac{dy}{dt} + y = K u\]

dove \(y\) è la ‘deviazione’ della variabile di processo da uno stato stazionario nominale e \(u\) è la deviazione della variabile manipolata da uno stato stazionario nominale. Per il laboratorio di controllo della temperatura assegneremo le variabili di deviazione come segue:

\[\begin{align*} y & = T_1 - T_{ambient} \\ u & = Q_1 \end{align*}\]

Il parametro \(K\) è il guadagno del processo che può essere stimato come il rapporto tra la variazione di stato stazionario di \(y\) dovuta a una variazione di stato stazionario di \(u\). Il parametro \(\tau\) è la “costante di tempo” del primo ordine che può essere stimata come il tempo necessario per raggiungere il 63,2% della variazione di stato stazionario della produzione per ottenere una variazione di stato stazionario di \(u\).

def model_first_order(param, plot=False):
    # access parameter values
    K, tau = param

    # simulation in deviation variables
    u = lambda ti: np.interp(ti, t, Q1)
    def deriv(y, ti):
        dydt  = (K*u(ti) - y)/tau
        return dydt
    y = odeint(deriv, 0, t)[:,0]

    # comparing to experimental data
    T_ambient = T1[0]
    T1_pred = y + T_ambient
    if plot:
        print("K =", K, "tau =", tau)
        plot_data(t, T1, T1_pred, Q1)
    
    return np.linalg.norm(T1_pred - T1)
    
param_first_order = [0.62, 180.0]
model_first_order(param_first_order, plot=True)

K = 0.62 tau = 180.0

24.649520390255464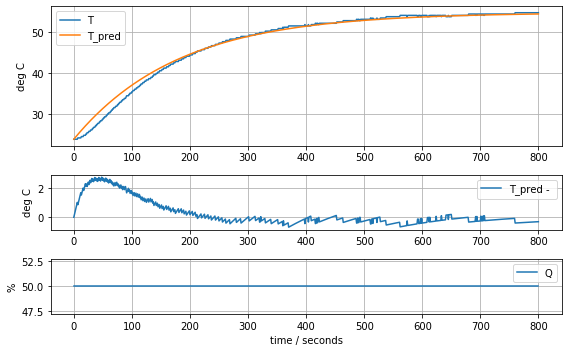

results = minimize(model_first_order, param_first_order, method='nelder-mead')
param_first_order = results.x
model_first_order(param_first_order, plot=True)

K = 0.6370841237049034 tau = 199.8617397701267

20.651093155278453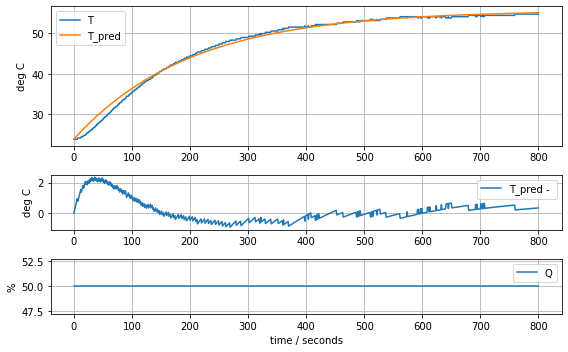

Modello lineare del primo ordine con ritardo temporale

La cella di codice qui sotto

def model_first_order_time_delay(param, plot=False):
    # access parameter values
    K, tau, tdelay = param
    
    # simulation in deviation variables
    u = lambda ti: np.interp(ti, t, Q1, left=0)
    def deriv(y, ti):
        dydt  = (K*u(ti-tdelay) - y)/tau
        return dydt
    y = odeint(deriv, 0, t)[:,0]

    # comparing to experimental data
    T_ambient = T1[0]
    T1_pred = y + T_ambient
    if plot:
        print("K =", K, "tau =", tau, "tdelay =", tdelay)
        plot_data(t, T1, T1_pred, Q1)
    
    return np.linalg.norm(T1_pred - T1)

param_first_order_time_delay = [0.62, 160.0, 15]
model_first_order_time_delay(param_first_order_time_delay, plot=True)

K = 0.62 tau = 160.0 tdelay = 15

16.12137889182889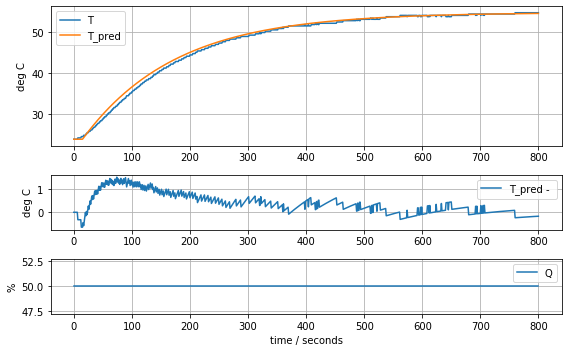

results = minimize(model_first_order_time_delay, param_first_order_time_delay, method='nelder-mead')
param_first_order_time_delay = results.x
model_first_order_time_delay(param_first_order_time_delay, plot=True)

K = 0.6228198545524255 tau = 167.7567962566444 tdelay = 20.18136187851927

6.290512704413097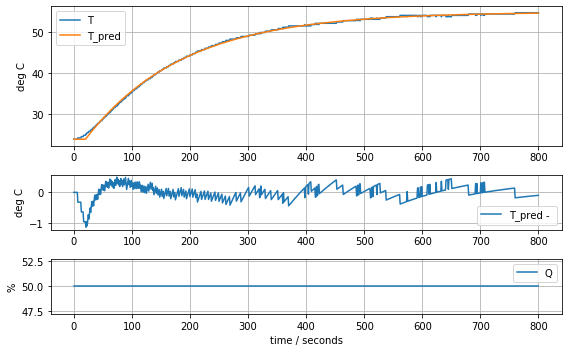

Modellazione basata su principi primi

Bilancio energetico del primo ordine per un riscaldatore

Supponendo che il gruppo riscaldatore/sensore possa essere descritto come una massa a temperatura uniforme che scambia calore con l’ambiente circostante, si ottiene un modello lineare del primo ordine.

\[C_p\frac{dT_{1}}{dt} = U_a (T_{amb} - T_{1}) + P Q_1\]

Il modello può essere riorganizzato nella forma di un sistema del primo ordine con costante di tempo \(\tau\) e guadagno \(K\)

\[\underbrace{\frac{C_p}{U_a}}_{\tau}\underbrace{\frac{d(T_1 - T_{amb})}{dt}}_{\frac{dy}{dt}} + \underbrace{T_1 - T_{amb}}_y = \underbrace{\frac{P}{U_a}}_K \underbrace{Q_1}_u\]

Utilizzando i risultati precedenti si ottengono stime per \(K\) e \(\tau\).

\[\begin{align*} K = \frac{P}{U_a} & \implies U_a = \frac{P}{K} = \frac{0.04}{0.62} = 0.065 \text{ watts/deg C} \\ \tau = \frac{C_p}{U_a} & \implies C_p = \tau U_a = \frac{\tau P}{K} = \frac{186 \times 0.04}{0.62} = 12 \text{ J/deg C} \end{align*}\]

P = 0.04

K, tau = param_first_order

Ua = P/K
print("Heat transfer coefficient Ua =", Ua, "watts/degree C")

Cp = tau*P/K
print("Heat capacity =", Cp, "J/deg C")

Heat transfer coefficient Ua = 0.06278605683560866 watts/degree C
Heat capacity = 12.548530552470801 J/deg C

def model_heater(param, plot=False):
    # access parameter values
    T_ambient, Cp, Ua = param
    
    P1 = 0.04

    # simulation in deviation variables
    u = lambda ti: np.interp(ti, t, Q1)
    def deriv(TH1, ti):
        dT1  = (Ua*(T_ambient - TH1) + P1*u(ti))/Cp
        return dT1
    T1_pred = odeint(deriv, T_ambient, t)[:,0]

    # comparing to experimental data
    if plot:
        print("Cp =", Cp, "Ua =", Ua)
        plot_data(t, T1, T1_pred, Q1)
    
    return np.linalg.norm(T1_pred - T1)

param_heater = [T1[0], Cp, Ua]
model_heater(param_heater, plot=True)

Cp = 12.548530552470801 Ua = 0.06278605683560866

20.651088966149587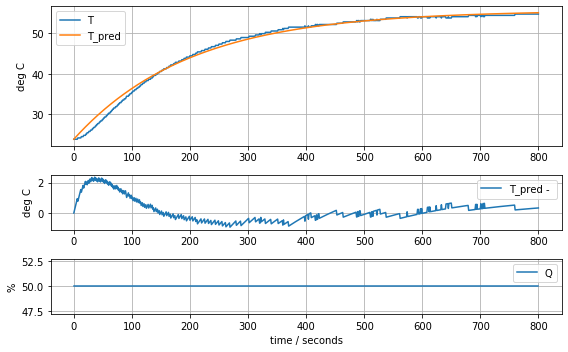

results = minimize(model_heater, param_heater, method='nelder-mead')
param_heater = results.x
model_heater(param_heater, plot=True)

Cp = 10.313205580961114 Ua = 0.05862920031801483

10.630933447435487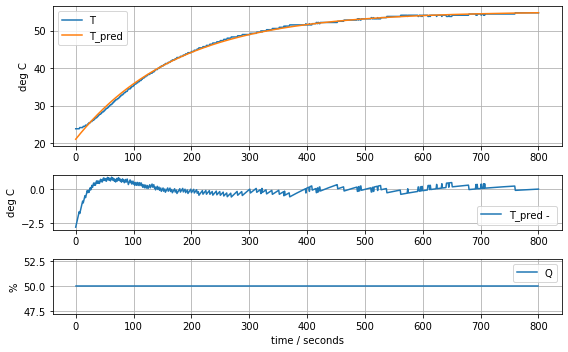

Modello a due stati

\[\begin{align*} C_p^H \frac{dT_{H,1}}{dt} & = U_a(T_{amb} - T_{H,1}) + U_c(T_{S,1} - T_{H,1}) + P_1Q_1 \\ C_p^S \frac{dT_{S,1}}{dt} & = U_c(T_{H,1} - T_{S,1}) \end{align*}\]

def model_heater_sensor(param, plot=False):
    # access parameter values
    T_ambient, Cp_H, Cp_S, Ua, Uc = param
    
    P1 = 0.04

    # simulation in deviation variables
    u = lambda ti: np.interp(ti, t, Q1)
    def deriv(T, ti):
        T_H1, T_S1 = T
        dT_H1 = (Ua*(T_ambient - T_H1) + Uc*(T_S1 - T_H1) + P1*u(ti))/Cp_H
        dT_S1 = Uc*(T_H1 - T_S1)/Cp_S
        return [dT_H1, dT_S1]
    T1_pred = odeint(deriv, [T_ambient, T_ambient], t)[:,1]

    # comparing to experimental data
    
    if plot:
        print(param)
        plot_data(t, T1, T1_pred, Q1)
    
    return np.linalg.norm(T1_pred - T1)

param_heater_sensor = [T1[0], Cp, Cp/5, Ua, Ua]
model_heater_sensor(param_heater_sensor, plot=True)

[23.81, 12.548530552470801, 2.50970611049416, 0.06278605683560866, 0.06278605683560866]

89.2722844989071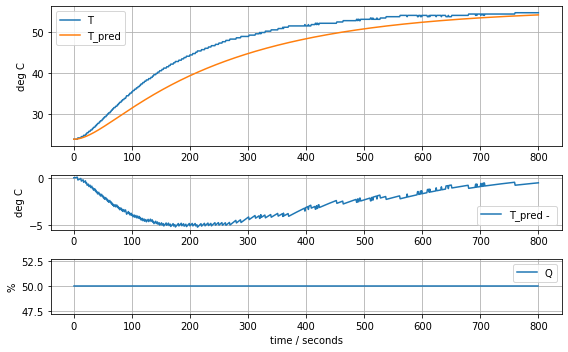

results = minimize(model_heater_sensor, param_heater_sensor, method='nelder-mead')
param_heater_sensor = results.x
model_heater_sensor(param_heater_sensor, plot=True)

[23.71861419  6.88125133  2.74272516  0.06428723  0.07897125]

4.554156209522013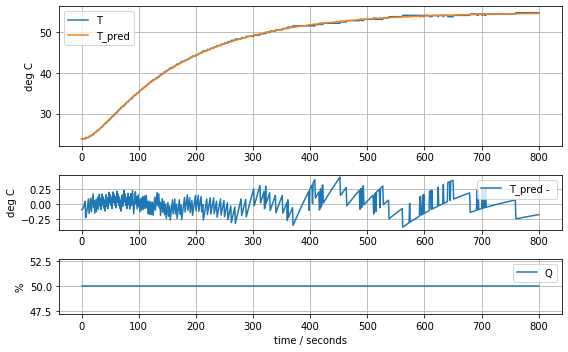

Due riscaldatori, modello a quattro stati

\[\begin{align*} C_p^H \frac{dT_{H,1}}{dt} & = U_a(T_{amb} - T_{H,1}) + U_b(T_{H,2} - T_{H,1}) + U_c(T_{S,1} - T_{H,1}) + P_1Q_1 \\ C_p^S \frac{dT_{S,1}}{dt} & = U_c(T_{H,1} - T_{S,1}) \\ C_p^H \frac{dT_{H,2}}{dt} & = U_a(T_{amb} - T_{H,2}) + U_b(T_{H,1} - T_{H,2}) + U_c(T_{S,2} - T_{H,2}) + P_2Q_2 \\ C_p^S \frac{dT_{S,2}}{dt} & = U_c(T_{H,2} - T_{S,2}) \end{align*}\]

def model_complete(param, plot=False):
    # access parameter values
    T_ambient, Cp_H, Cp_S, Ua, Ub, Uc = param
    
    P1 = 0.04

    # simulation in deviation variables
    u = lambda ti: np.interp(ti, t, Q1)
    def deriv(T, ti):
        T_H1, T_S1, T_H2, T_S2 = T
        dT_H1 = (Ua*(T_ambient - T_H1) + Ub*(T_H2 - T_H1) + Uc*(T_S1 - T_H1) + P1*u(ti))/Cp_H
        dT_S1 = Uc*(T_H1 - T_S1)/Cp_S
        dT_H2 = (Ua*(T_ambient - T_H2) + Ub*(T_H1 - T_H2) + Uc*(T_S2 - T_H2))/Cp_H
        dT_S2 = Uc*(T_H2 - T_S2)/Cp_S
        return [dT_H1, dT_S1, dT_H2, dT_S2]
    T_pred = odeint(deriv, [T_ambient, T_ambient, T_ambient, T_ambient], t)
    T1_pred = T_pred[:,1]
    T2_pred = T_pred[:,3]

    # comparing to experimental data
    if plot:
        print(param)
        plot_data(t, T1, T1_pred, Q1)
        plot_data(t, T2, T2_pred, Q1)
    
    return (np.linalg.norm(T1_pred - T1) + np.linalg.norm(T2_pred - T2))/2

param_complete = [T1[0], Cp, Cp/5, Ua, Ua, Ua]
model_complete(param_complete, plot=True)

[23.81, 12.548530552470801, 2.50970611049416, 0.06278605683560866, 0.06278605683560866, 0.06278605683560866]

143.87441921309681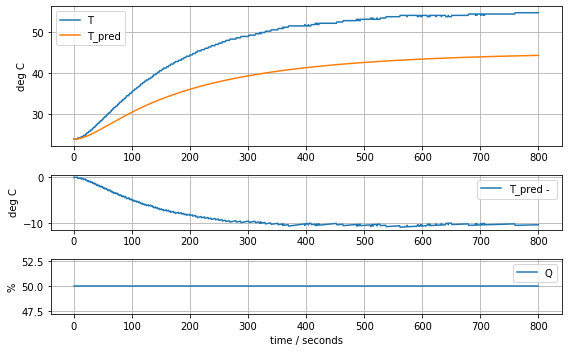

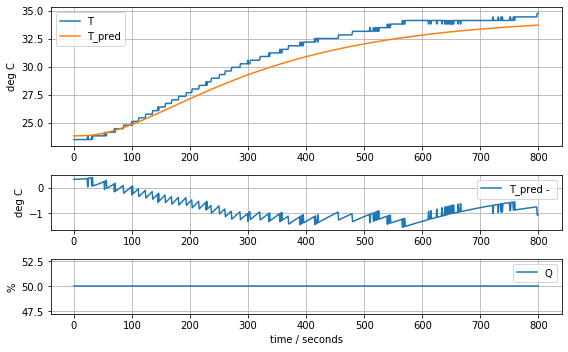
results = minimize(model_complete, param_complete, method='nelder-mead')
param_complete = results.x
model_complete(param_complete, plot=True)

[23.60707391  6.92707544  1.61783224  0.04676309  0.02633501  0.04303801]

4.441799745669341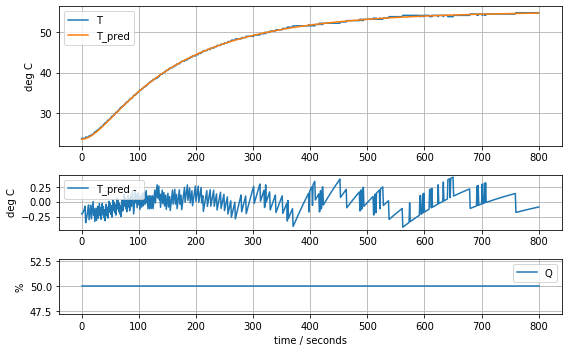

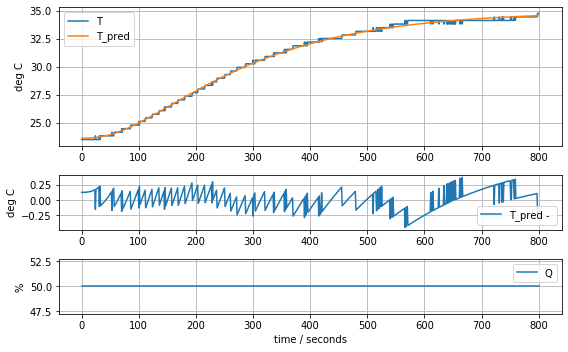
Conseguenze

def model_complete(param, plot=False):
    # access parameter values
    T_ambient, Cp_H, Cp_S, Ua, Ub, Uc = param
    
    P1 = 0.04

    # simulation in deviation variables
    u = lambda ti: np.interp(ti, t, Q1)
    def deriv(T, ti):
        T_H1, T_S1, T_H2, T_S2 = T
        dT_H1 = (Ua*(T_ambient - T_H1) + Ub*(T_H2 - T_H1) + Uc*(T_S1 - T_H1) + P1*u(ti))/Cp_H
        dT_S1 = Uc*(T_H1 - T_S1)/Cp_S
        dT_H2 = (Ua*(T_ambient - T_H2) + Ub*(T_H1 - T_H2) + Uc*(T_S2 - T_H2))/Cp_H
        dT_S2 = Uc*(T_H2 - T_S2)/Cp_S
        return [dT_H1, dT_S1, dT_H2, dT_S2]
    T_pred = odeint(deriv, [T_ambient, T_ambient, T_ambient, T_ambient], t)
    T1_pred = T_pred[:,1]
    T2_pred = T_pred[:,3]

    # comparing to experimental data
    if plot:
        print(param)
        plot_data(t, T_pred[:,1], T_pred[:,0], Q1)
        plot_data(t, T_pred[:,3], T_pred[:,2], Q1)
    
    return (np.linalg.norm(T1_pred - T1) + np.linalg.norm(T2_pred - T2))/2

model_complete(param_complete, plot=True)

[23.60707391  6.92707544  1.61783224  0.04676309  0.02633501  0.04303801]

4.441799745669341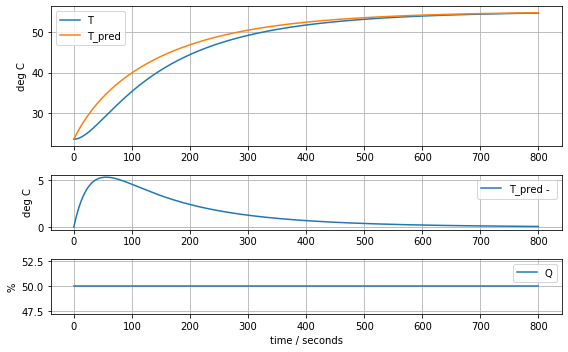

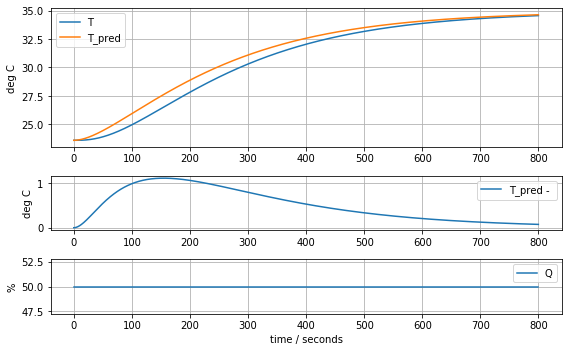
Modello Spazio-Stato

Richiamo delle equazioni del modello

\[\begin{align*} C_p^H \frac{dT_{H,1}}{dt} & = U_a(T_{amb} - T_{H,1}) + U_b(T_{H,2} - T_{H,1}) + U_c(T_{S,1} - T_{H,1}) + P_1Q_1 \\ C_p^S \frac{dT_{S,1}}{dt} & = U_c(T_{H,1} - T_{S,1}) \\ C_p^H \frac{dT_{H,2}}{dt} & = U_a(T_{amb} - T_{H,2}) + U_b(T_{H,1} - T_{H,2}) + U_c(T_{S,2} - T_{H,2}) + P_2Q_2 \\ C_p^S \frac{dT_{S,2}}{dt} & = U_c(T_{H,2} - T_{S,2}) \end{align*}\]

Normalizzazione delle derivate

\[\begin{align*} C_p^H \frac{dT_{H,1}}{dt} & = -(U_a + U_b + U_c)T_{H,1} + U_c T_{S,1} + U_b T_{H,2} + U_a T_{amb} + P_1Q_1 \\ C_p^S \frac{dT_{S,1}}{dt} & = U_c T_{H,1} - U_c T_{S,1}) \\ C_p^H \frac{dT_{H,2}}{dt} & = U_b T_{H,1} - (U_a + U_b + U_c) T_{H,2} + U_c T_{S,2} + U_aT_{amb} + P_2Q_2 \\ C_p^S \frac{dT_{S,2}}{dt} & = U_c T_{H,2} - U_c T_{S,2} \end{align*}\]

Raccolta dei termini sul lato destro

\[\begin{align*} \frac{dT_{H,1}}{dt} & = -\frac{(U_a + U_b + U_c)}{C_p^H} T_{H,1} + \frac{U_c}{C_p^H} T_{S,1} + \frac{U_b}{C_p^H} T_{H,2} + \frac{U_a}{C_p^H} T_{amb} + \frac{P_1}{C_p^H} Q_1 \\ \frac{dT_{S,1}}{dt} & = \frac{U_c}{C_p^S} T_{H,1} - \frac{U_c}{C_p^S} T_{S,1} \\ \frac{dT_{H,2}}{dt} & = \frac{U_b}{C_p^H} T_{H,1} - \frac{(U_a + U_b + U_c)}{C_p^H} T_{H,2} + \frac{U_c}{C_p^H} T_{S,2} + \frac{U_a}{C_p^H} T_{amb} + \frac{P_2}{C_p^H} Q_2 \\ \frac{dT_{S,2}}{dt} & = \frac{U_c}{C_p^S} T_{H,2} - \frac{U_c}{C_p^S} T_{S,2} \end{align*}\]

Modello dello spazio degli stati

\[ \underbrace{\begin{bmatrix} \frac{dT_{H,1}}{dt} \\ \frac{dT_{S,1}}{dt} \\ \frac{T_{H,2}}{dt} \\ \frac{T_{S,2}}{dt} \end{bmatrix}}_{\frac{dx}{dt}} = \underbrace{\begin{bmatrix} -\frac{(U_a + U_b + U_c)}{C_p^H} & \frac{U_c}{C_p^H} & \frac{U_b}{C_p^H} & 0 \\ \frac{U_c}{C_p^S} & - \frac{U_c}{C_p^S} & 0 & 0 \\ \frac{U_b}{C_p^H} & 0 & - \frac{(U_a + U_b + U_c)}{C_p^H} & \frac{U_c}{C_p^H} \\ 0 & 0 & \frac{U_c}{C_p^S} & - \frac{U_c}{C_p^S} \end{bmatrix}}_A \underbrace{\begin{bmatrix} T_{H,1} \\ T_{S,1} \\ T_{H,2} \\ T_{S,2} \end{bmatrix}}_x + \underbrace{\begin{bmatrix} \frac{P_1}{C_p^H} & 0 \\ 0 & 0 \\ 0 & \frac{P_2}{C_p^H} \\ 0 & 0 \end{bmatrix}}_B \underbrace{\begin{bmatrix} Q_1 \\ Q_2 \end{bmatrix}}_u + \underbrace{\begin{bmatrix} \frac{U_a}{C_p^H} \\ 0 \\ \frac{U_a}{C_p^H} \\ 0 \end{bmatrix}}_E \underbrace{T_{amb}}_d\]

\[\underbrace{\begin{bmatrix} T_1 \\ T_2 \end{bmatrix}}_y = \underbrace{\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix }}_C \underbrace{\begin{bmatrix} T_{H,1} \\ T_{S,1} \\ T_{H,2} \\ T_{S,2} \end{bmatrix}}_x + \ underbrace{\begin{bmatrix} 0 & 0 \\ 0 & 0\end{bmatrix}}_D \underbrace{\begin{bmatrix} Q_1 \\ Q_2 \end{bmatrix}}_u\]

Formulazione matriciale/vettoriale

\[\begin{align*} \frac{dx}{dt} & = A x + B u + E d \\ y & = C x + D u \end{align*}\]

P1 = 0.04
P2 = 0.02

T_ambient, Cp_H, Cp_S, Ua, Ub, Uc = param_complete

A = np.array([[-(Ua + Ub + Uc)/Cp_H, Uc/Cp_H, Ub/Cp_H, 0],
     [Uc/Cp_S, -Uc/Cp_S, 0, 0],
     [Ub/Cp_H, 0, -(Ua + Ub + Uc)/Cp_H, Uc/Cp_H],
     [0, 0, Uc/Cp_S, -Uc/Cp_S]])

B = np.array([[P1/Cp_H, 0], [0, 0], [0, P2/Cp_H], [0, 0]])

C = np.array([[0, 1, 0, 0], [0, 0, 0, 1]])

D = np.array([[0, 0], [0, 0]])

E = np.array([[Ua/Cp_H], [0], [Ua/Cp_H], [0]])

Costanti di tempo

eval, evec = np.linalg.eig(A)
-1/eval

array([191.1942343 ,  96.34592497,  27.18108829,  29.12414895])

evec

array([[ 0.44286448, -0.36815989, -0.25289296, -0.19739009],
       [ 0.551245  , -0.60370381,  0.66033715,  0.67899717],
       [ 0.44286448,  0.36815989,  0.25289296, -0.19739009],
       [ 0.551245  ,  0.60370381, -0.66033715,  0.67899717]])

Mettersi al lavoro

from control import *
from control.matlab import *

ss = StateSpace(A, B, C, D)

ss

A = [[-0.01676553  0.00621301  0.00380175  0.        ]
 [ 0.02660227 -0.02660227  0.          0.        ]
 [ 0.00380175  0.         -0.01676553  0.00621301]
 [ 0.          0.          0.02660227 -0.02660227]]

B = [[0.00577444 0.        ]
 [0.         0.        ]
 [0.         0.00288722]
 [0.         0.        ]]

C = [[0. 1. 0. 0.]
 [0. 0. 0. 1.]]

D = [[0. 0.]
 [0. 0.]]

y,t = step(ss, input=0)
plt.plot(t,y)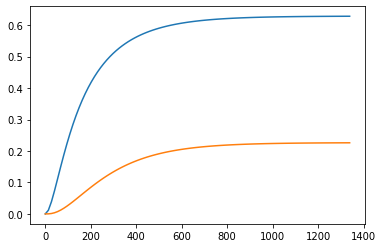

pole(ss)

array([-0.00523028, -0.01037927, -0.03679029, -0.03433577])

tf(ss,)

\[\begin{bmatrix}\frac{0.0001536 s^2}{s^4 + 0.03957 s^3 + 0.0001796 s^2}&\frac{7.681 \times 10^{-5} s^2}{s^4 + 0.03957 s^3 + 0.0001796 s^2}\\\frac{5.84 \times 10^{-7} s + 1.554 \times 10^{-8}}{s^4 + 0.08674 s^3 + 0.002428 s^2 + 2.358 \times 10^{-5} s + 6.858 \times 10^{-8}}&\frac{7.681 \times 10^{-5} s^2 + 3.331 \times 10^{-6} s + 2.156 \times 10^{-8}}{s^4 + 0.08674 s^3 + 0.002428 s^2 + 2.358 \times 10^{-5} s + 6.858 \times 10^{-8}}\\ \end{bmatrix}\]