import pandas as pd
df = pd.read_csv('data/step-test-data.csv')
df = df.set_index('Time')
df.plot(grid=True)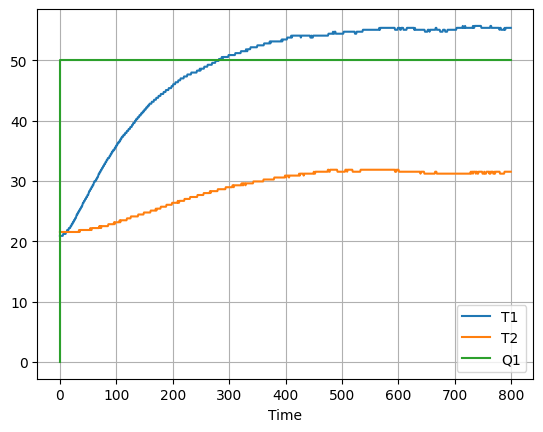
Adattamento dei dati dei test di fase ai modelli empirici
Leggi il file dati
Parametro
Adattamento dei dati di modifica del passo a un modello del primo ordine
Per un sistema lineare del primo ordine inizialmente allo stato stazionario, la risposta a una variazione dell’ingresso a gradino a \(t=0\) è data da
\[y(t) = y(0) + K(1 - e^{-t/\tau}) \Delta U\]
dove \(\Delta U\) è l’entità del cambiamento graduale. Conversione nella notazione utilizzata per il laboratorio di controllo della temperatura dove \(y(t) = T_1(t)\) e \(\Delta U = \Delta Q_1\)
\[T_1(t) = T_1(0) + K_1(1 - e^{-t/\tau_1}) \Delta Q_1\]
le celle seguenti forniscono le stime iniziali per il guadagno in stato stazionario \(K_1\) e la costante di tempo \(\tau_1\).
Lettura dei dati salvati
df[['Q1','T1','T2']].plot(grid=True)
Stima del guadagno e della costante di tempo
Nel limite \(t\rightarrow\infty\) diventa il modello del primo ordine
\[T_1(\infty) = T_1(0) + K_1\Delta Q_1\]
che fornisce un metodo per stimare \(K_1\)
\[K_1 = \frac{T_1(\infty) - T_1(0)}{\Delta Q_1}\]
Questi calcoli vengono eseguiti di seguito dove utilizziamo la prima e l’ultima misurazione di \(T_1\) come stime di \(T_1(0)\) e \(T_1(\infty)\), rispettivamente.
T1 = df['T1']
Q1 = df['Q1']
DeltaT1 = max(T1) - min(T1)
DeltaQ1 = Q1.mean()
K1 = DeltaT1/DeltaQ1
print("K1 is approximately", K1)K1 is approximately 0.6968700000000001# find when the increase in T1 gets larger than 63.2% of the final increase
i = (T1 - T1.min()) > 0.632*(T1.max()-T1.min())
tau1 = T1.index[i].min()
print("tau1 is approximately", tau1, "seconds")tau1 is approximately 163.0 secondsimport matplotlib.pyplot as plt
import numpy as np
exp = np.exp
t = df.index
T1_est = T1.min() + K1*(1 - exp(-t/tau1))*DeltaQ1
plt.figure(figsize=(10,5))
ax = plt.subplot(2,1,1)
df['T1'].plot(ax = ax, grid=True)
plt.plot(t,T1_est)
plt.title('Step Test Data Compared to Model')
plt.subplot(2,1,2)
plt.plot(t,T1_est-T1)
plt.grid()
plt.title('Residual Error')Text(0.5, 1.0, 'Residual Error')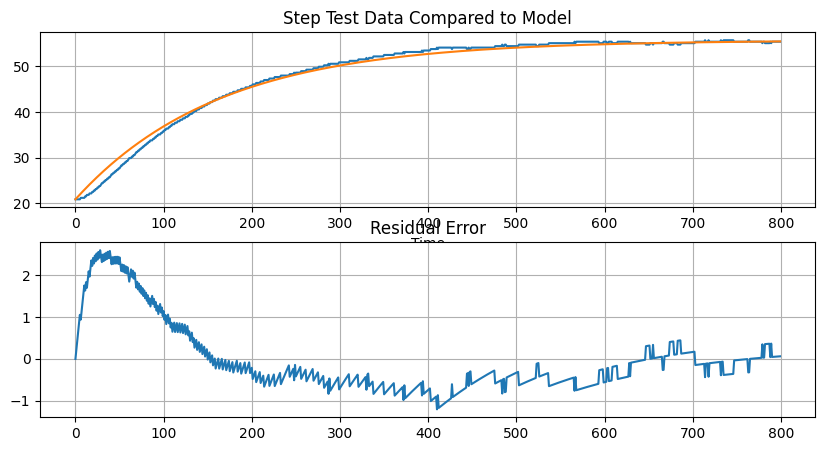
Un modello del primo ordine cattura determinate caratteristiche e fornisce un risultato ragionevolmente buono quando il sistema si avvicina a un nuovo stato stazionario. Il problema, tuttavia, è che per il controllo abbiamo bisogno di un buon modello durante il transitorio iniziale. È qui che il modello del primo ordine crolla e prevede una risposta qualitativamente diversa da quella che osserviamo.
Primo Ordine più Ritardo (o Tempo Morto)
\[T_1(t) = T_1(0) + K (1-e^\frac{t-\theta}{\tau}) Q_{step}\]
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from ipywidgets import interact
df = pd.read_csv('data/step-test-data.csv')
df = df.set_index('Time')
T1 = df['T1']
Q1 = df['Q1']
t = df.index
DeltaT1 = max(T1) - min(T1)
DeltaQ1 = Q1.mean()
K1 = DeltaT1/DeltaQ1
i = (T1 - T1.min()) > 0.632*(T1.max()-T1.min())
tau1 = T1.index[i].min()
def fopdt(K=K1, tau=tau1, theta=0, T10=T1.min()):
def Q1(t):
return 0 if t < 0 else DeltaQ1
Q1vec = np.vectorize(Q1)
T1_fopdt = T10 + K*(1-np.exp(-(t-theta)/tau))*Q1vec(t-theta)
plt.figure(figsize=(10,5))
plt.subplot(2,1,1)
plt.plot(t,T1_fopdt)
plt.plot(t,df['T1'])
plt.subplot(2,1,2)
plt.plot(t,T1_fopdt - T1)
plt.show()
interact(fopdt,K=(0,1,.001),tau=(50,200,.5),theta=(0,50,.5),T10=(15,25,.1))<function __main__.fopdt(K=0.6968700000000001, tau=163.0, theta=0, T10=20.9)>Secondo ordine
SEMD Equaz. 5-48
\[T_1(t) = T_1(0) + K\left(1 - \frac{\tau_1 e^{-t/\tau_1} - \tau_2 e^{-t/\tau_2}}{\tau_1 - \ \tau_2}\right)Q_1(t)\]
from scipy.optimize import least_squares
import numpy as np
Qmax = 50
def f(x):
K,tau1,tau2,T10 = x
t = df.index
exp = np.exp
Tpred = T10 + K*(1 - (tau1*exp(-t/tau1) - tau2*exp(-t/tau2))/(tau1-tau2))*Qmax
resid = df['T1'] - Tpred
return resid
ic = [0.86,40,130,20]
r = least_squares(f,ic,bounds=(0,np.inf))
r.xarray([ 0.69537389, 19.68872647, 141.40950924, 20.91093839])E la funzione di trasferimento risultante è:
\[ G_1(s) = \frac{0,70}{(20s + 1)(141s + 1)} \]