| #### BARRA LATERALE - Esplorazione dei criteri di prestazione del sistema di controllo |
| ### 1. Stabilità |
| #### Definizione e importanza La stabilità è la pietra angolare delle prestazioni del sistema di controllo. Un sistema è considerato stabile se, in risposta ad un input limitato, produce un output limitato. In termini pratici, ciò significa che il sistema non mostrerà comportamenti fuori controllo o oscillazioni che crescono indefinitamente nel tempo. |
| #### Rappresentazione matematica - Stabilità BIBO: un sistema è stabile con input limitato e output limitato (BIBO) se ogni input limitato produce un output limitato. Matematicamente, se $ |x(t)| < M < $ per tutti $ t $, quindi $ |y(t)| < N < $ per tutti $ t $, dove $ x(t) $ è l’input, $ y(t) $ è l’output e $ M, N $ sono costanti. - Criterio di Routh-Hurwitz: questo criterio fornisce un metodo per determinare la stabilità di un sistema esaminando la posizione dei poli della funzione di trasferimento del sistema. Se tutti i poli si trovano nella metà sinistra del piano complesso, il sistema è stabile. |
| #### Considerazioni pratiche - Margini di stabilità: nella progettazione, non si tratta solo di raggiungere la stabilità, ma di garantire un grado di robustezza nella stabilità, noto come margini di stabilità. Questi margini indicano quanto possono variare i parametri di un sistema prima che diventi instabile. |
| ### 2. Risposta transitoria |
| #### Caratterizzazione del comportamento transitorio La risposta transitoria si riferisce alla reazione del sistema da uno stato iniziale al raggiungimento del suo stato stazionario. Le caratteristiche chiave includono: - Tempo di salita: tempo impiegato dalla risposta per salire dal 10% al 90% del suo valore finale. - Tempo di assestamento: tempo impiegato dalla risposta per rimanere entro una certa percentuale (comunemente 2% o 5%) del valore finale. - Overshoot: la quantità di cui la risposta supera il valore finale. - Rapporto di smorzamento: una misura delle oscillazioni nella risposta. |
| #### Obiettivi di progettazione - Velocità di risposta: un tempo di salita più rapido è spesso auspicabile, ma può portare a un aumento del superamento. - Controllo dell’oscillazione: riduce al minimo il superamento e garantisce che il sistema si assesti rapidamente senza oscillazioni prolungate. |
| ### 3. Precisione allo stato stazionario |
| #### Comprendere lo stato stazionario Una volta che gli effetti transitori sono diminuiti, il sistema entra in uno stato stazionario. In questo caso, l’output dovrebbe idealmente corrispondere il più fedelmente possibile al valore comandato. |
| #### Misure di accuratezza in regime stazionario - Metriche di errore: le misure comuni includono errore in stato stazionario, errore di tracciamento e costanti di errore come costanti di errore di posizione, velocità e accelerazione. - Tipo di sistema ed errore: il tipo di sistema di controllo (Tipo 0, Tipo 1, ecc.) determina la sua capacità di gestire diversi tipi di errori stazionari, in particolare per ingressi a gradino, rampa e parabolici. |
| #### Progettare per la precisione - Controllo del feedback: l’integrazione del feedback riduce efficacemente l’errore in stato stazionario. - Controllo integrale: l’aggiunta di un componente integrale può eliminare l’errore di stato stazionario per determinati tipi di ingressi. |
| ### 4. Sensibilità e robustezza |
| #### Resilienza alle variazioni La sensibilità e la robustezza misurano la capacità di un sistema di mantenere le prestazioni nonostante i cambiamenti nei parametri del sistema o nelle condizioni ambientali. |
| #### Analisi quantitativa - Funzione sensibilità: questa funzione quantifica la sensibilità dell’output del sistema alle modifiche di un particolare parametro. - Tecniche di progettazione robusta: metodi come H-infinito e μ-sintesi vengono utilizzati per progettare sistemi che mantengono le prestazioni in una gamma di incertezze. |
| #### Applicazione pratica - Analisi del caso peggiore: valutazione delle prestazioni del sistema in condizioni di variazioni estreme per garantire un funzionamento affidabile. |
| ### 5. Rifiuto del disturbo |
| #### Minimizzare l’impatto esterno I sistemi di controllo spesso operano in ambienti con disturbi esterni. Un’efficace reiezione dei disturbi riduce al minimo l’impatto di questi disturbi sull’uscita del sistema. |
| #### Valutazione del rifiuto dei disturbi - Risposta transitoria al disturbo: osservazione della rapidità ed efficacia con cui il sistema mitiga l’impatto di un disturbo. - Errore in stato stazionario dovuto a disturbo: garantire che, in stato stazionario, il disturbo abbia un impatto minimo o nullo sull’uscita. |
| #### Strategie di controllo - Controllo feedforward: Anticipare i disturbi e compensarli prima che incidano sul sistema. - Controllo feedback: regolazione del comportamento del sistema in risposta ai disturbi rilevati nell’uscita. |
| — FINE DELLA BARRA LATERALE |
| ## Transizione alle specifiche quantitative |
| Nella progettazione del sistema di controllo, spesso iniziamo specificando: - il transitorio desiderato - e precisione in condizioni stazionarie. |
| Una volta progettato un sistema con queste specifiche, ne valutiamo le prestazioni in termini di robustezza e reiezione ai disturbi. |
| Nota: la ricerca attuale sulla progettazione dei sistemi di controllo si sta evolvendo verso l’inclusione della sensibilità e della robustezza nella fase di progettazione iniziale stessa. Tuttavia, questa è ancora un’area emergente e non ampiamente incorporata nei programmi di studio standard. Ci concentreremo sul modo classico di progettazione del controllo e questo fornirà la base per comprendere robustezza e sensibilità. |
| ### Approccio classico nella progettazione dei sistemi di controllo |
| Nella metodologia tradizionale dell’ingegneria dei sistemi di controllo, l’attenzione principale è inizialmente posta sulla precisione transitoria e stazionaria. Questo approccio metodico comprende diversi passaggi chiave: |
| 1. Garanzia della stabilità del sistema: questa fase iniziale prevede l’applicazione di strumenti analitici come il criterio di stabilità di Routh. Questi strumenti vengono utilizzati per accertare le condizioni di stabilità del sistema determinando gli intervalli specifici di parametri che garantiscono la stabilità. La stabilità del sistema è un requisito primario. Se questo non regge tutto il resto non ha importanza. |
| 2. Ottimizzazione per prestazioni transitorie e stazionarie: il passaggio successivo è l’attenta selezione dei parametri di sistema. Questi parametri vengono scelti all’interno dei domini di stabilità identificati con l’obiettivo di raggiungere i livelli desiderati di accuratezza transitoria e stazionaria. Questo processo di selezione è fondamentale affinché il sistema risponda efficacemente ai cambiamenti e mantenga la precisione nel tempo. Questa è la specifica quantitativa delle prestazioni del sistema. |
| 3. Valutazione della robustezza e delle capacità di reiezione ai disturbi: la fase finale prevede una simulazione approfondita del sistema di controllo. Questa simulazione è fondamentale per valutare se il sistema soddisfa gli standard predefiniti di robustezza e la sua capacità di respingere i disturbi. Se questi standard non vengono soddisfatti, si innesca una rivalutazione e una riprogettazione della strategia di controllo. Questa natura iterativa della progettazione riconosce che il raggiungimento di prestazioni ottimali spesso richiede molteplici aggiustamenti e perfezionamenti. |
| Seguendo questi passaggi, l’approccio classico garantisce un processo di sviluppo completo e iterativo, con l’obiettivo di creare un sistema di controllo stabile, accurato, robusto e in grado di respingere efficacemente i disturbi. |
| ### Metodologia di progettazione per il sistema di controllo: valutazione di stabilità, accuratezza e robustezza |
| 1. Identificazione dei domini di stabilità dei parametri: - Il passo iniziale nella progettazione di un sistema di controllo comporta la determinazione delle condizioni in cui il sistema rimarrà stabile. - Stabilità, nei sistemi di controllo, significa che il sistema non mostrerà un comportamento illimitato o irregolare in risposta a un dato input. - Per trovare queste condizioni, utilizziamo metodi analitici come il criterio di stabilità di Routh. Questo criterio aiuta a identificare i “domini” o intervalli di parametri del sistema (come guadagno, rapporto di smorzamento, ecc.) che garantiscono che il sistema rimanga stabile. - Ad esempio, potremmo risolvere problemi in cui manipoliamo uno o due parametri (come la regolazione del guadagno di un controller) per vedere come questi cambiamenti influiscono sulla stabilità del sistema. |
| 2. Garantire la precisione transitoria e stazionaria: - Una volta identificati i domini di stabilità, il passo successivo è affinare i parametri di sistema all’interno di questi domini. - Questo perfezionamento mira a raggiungere obiettivi prestazionali specifici legati al modo in cui il sistema risponde nel tempo (prestazioni transitorie) e alla precisione con cui mantiene il suo output nel lungo termine (prestazioni stazionarie). - L’accuratezza transitoria riguarda la rapidità e l’efficacia con cui il sistema risponde ai cambiamenti, mentre l’accuratezza allo stato stazionario si concentra su quanto l’output del sistema corrisponde all’output desiderato dopo che le fluttuazioni iniziali si sono stabilizzate. |
| 3. Valutazione della robustezza e del rifiuto dei disturbi: - Dopo aver soddisfatto i requisiti transitori e stazionari, torniamo alla configurazione originale del sistema. - Qui simuliamo il sistema in varie condizioni per valutarne la robustezza (quanto bene si comporta in diverse condizioni operative o variazioni dei parametri) e la sua capacità di respingere i disturbi (quanto bene mantiene le sue prestazioni in presenza di influenze esterne impreviste). - Se il sistema non riesce a soddisfare i criteri di robustezza o di reiezione ai disturbi, potrebbe essere necessario rivedere il processo di progettazione. Ciò potrebbe comportare la nuova regolazione dei parametri o addirittura la riprogettazione di alcuni aspetti del sistema. |
| Seguendo questo approccio strutturato, garantiamo che il sistema di controllo che progettiamo non solo sia stabile ma soddisfi anche specifici criteri di prestazione sia a breve che a lungo termine e sia resistente ai disturbi esterni e ai cambiamenti dei parametri interni. Questa valutazione globale è fondamentale per creare un sistema di controllo affidabile ed efficiente. |
| ## Esplorazione delle specifiche relative alle prestazioni transitorie |
| ### Sistemi di feedback unitario |
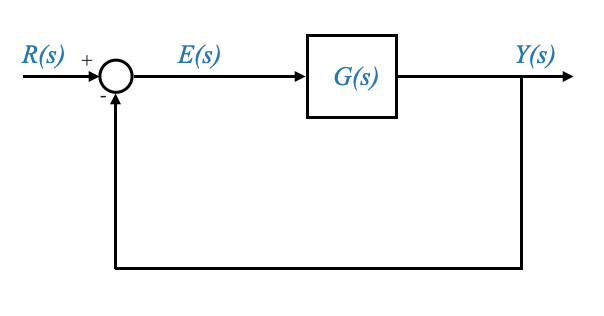
| Per semplicità, considereremo un sistema con feedback unitario, sebbene i principi si applichino anche ai sistemi con feedback non unitario. |
|
| - La funzione di trasferimento del sistema è: |
| \[ Y(s) / R(s) = G(s) / (1 + G(s)) \] |
| - Qui, $ Y(s) $ è l’output, $ R(s) $ è l’input e $ G(s) $ è la funzione di trasferimento del sistema. |
| ### Natura dei segnali di ingresso |
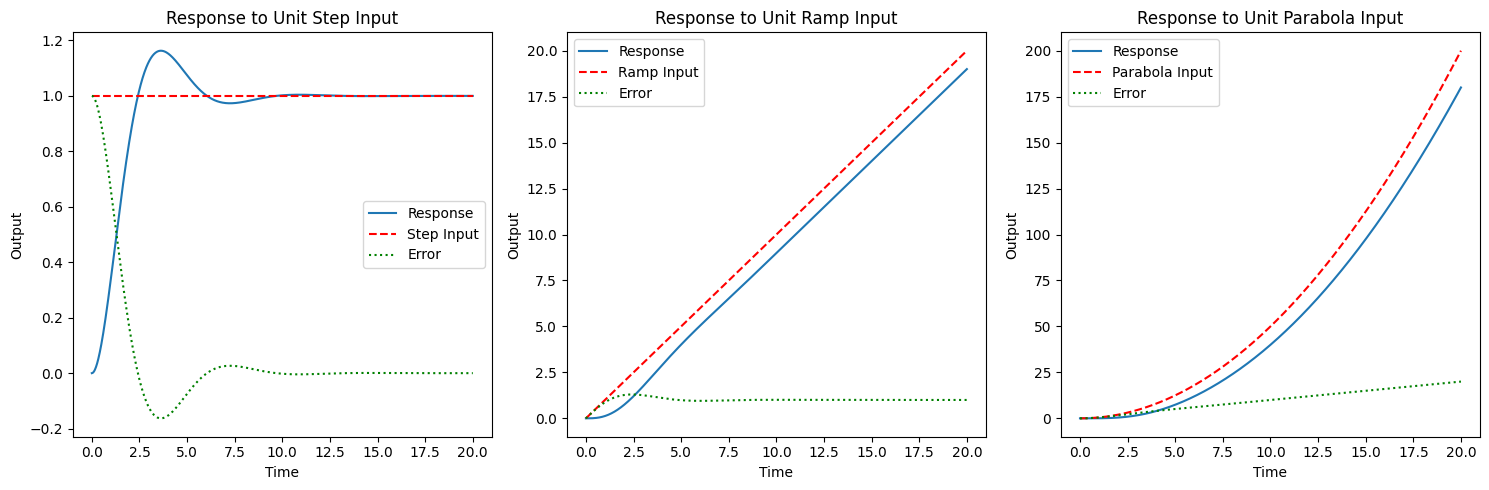
| Nei sistemi di controllo pratici, la natura del segnale di ingresso è imprevedibile. Pertanto, utilizziamo segnali di test standard (gradino, rampa, parabola) per progettare e valutare il sistema. Se il sistema funziona bene con questi segnali, dovrebbe funzionare bene con qualsiasi altro segnale. |
| Le prestazioni transitorie dipendono dai poli del sistema ed sono relativamente indipendenti dalla natura del segnale di ingresso. |
| Ad esempio, se i poli sono sulla sinistra, il transitorio si estinguerà. Il transitorio dipende quindi dalle caratteristiche del sistema e non dallo specifico ingresso. |
| In altre parole, nella progettazione del sistema di controllo, è fondamentale valutare come il sistema risponderà ai vari tipi di segnali di ingresso. Poiché non è pratico prevedere ogni possibile input che un sistema potrebbe incontrare nelle operazioni del mondo reale, utilizziamo input di test standard come parametri di riferimento. Questi includono, tra gli altri, segnali a gradino, rampa e parabolici. |
| - Inserimento graduale: si tratta di un cambiamento improvviso, in genere da zero a un valore fisso. È utile per osservare la reazione immediata del sistema e le sue caratteristiche di risposta transitoria. |
| - Ingresso rampa: questo ingresso aumenta linearmente nel tempo, rappresentando un setpoint in continua evoluzione. Aiuta a comprendere come il sistema tiene traccia di un input che varia gradualmente e può essere particolarmente rivelatore per i sistemi in cui il tasso di variazione dell’input è significativo. |
| - Ingresso parabolico: rappresenta uno scenario in cui l’input cambia a un ritmo accelerato, fornendo informazioni su come il sistema gestisce condizioni più complesse e in cambiamento dinamico. |
| La scelta di questi segnali di test non è arbitraria. Sono selezionati perché stimolano efficacemente diversi aspetti del comportamento del sistema. L’ingresso passo verifica la stabilità di base del sistema e la risposta transitoria. L’ingresso della rampa esamina la capacità del sistema di tenere il passo con un setpoint in continua evoluzione, che è fondamentale per monitorare le prestazioni. L’input parabolico, introducendo un cambiamento accelerato, sfida la reattività del sistema a input più complessi e dinamici. |
| Progettando un sistema di controllo che funzioni in modo soddisfacente con questi input di test standard, possiamo dedurre che probabilmente gestirà un’ampia gamma di input del mondo reale in modo efficace. Questo approccio semplifica il processo di progettazione riducendo l’infinita varietà di possibili input in una serie gestibile di test standard, ciascuno incentrato su un aspetto critico delle prestazioni del sistema. |
| ### Utilizzo dell’input passo per l’analisi della risposta transitoria |
| - Nel contesto dell’analisi della risposta transitoria, viene comunemente utilizzato lo step input, rappresentato da una funzione unit-step $ (t) $. - Il ragionamento alla base di questa scelta è che uno step input è particolarmente efficace nello stimolare tutte le modalità del sistema. Questa eccitazione completa consente un’osservazione e un’analisi dettagliate della risposta transitoria del sistema. È importante notare che la stabilità e le caratteristiche transitorie di un sistema di controllo sono determinate principalmente dalla posizione dei suoi poli, che sono proprietà intrinseche del sistema stesso, piuttosto che dalla natura del segnale di ingresso. Pertanto, utilizzando la forma più semplice di input di test, lo step input, possiamo valutare in modo efficiente il comportamento del sistema senza la necessità di forme di input più complesse. Questo approccio semplifica l’analisi fornendo comunque una comprensione approfondita delle dinamiche transitorie del sistema. |
| Per questo motivo, l’input unitario viene utilizzato per specificare quantitativamente le caratteristiche transitorie del sistema. Si noti inoltre che un’ampiezza maggiore non cambia la natura della risposta, cambierà solo l’ampiezza della risposta. |
|
| 🤔Domanda pop-up: Perché preferiamo un input a passi unitari per l’analisi transitoria? |
| Risposta: Un input a passi unitari semplifica l’analisi ed è efficace nell’attivare tutte le modalità del sistema, rendendolo ideale per osservare il comportamento transitorio del sistema. |
| ## Specifiche delle prestazioni in stato stazionario |
| ### Dipendenza dall’input e caratteristiche del sistema |
| A differenza delle prestazioni transitorie, la risposta allo stato stazionario dipende sia dalle caratteristiche del sistema che dalla natura del segnale di ingresso. Pertanto, un singolo tipo di segnale di ingresso potrebbe non essere sufficiente per caratterizzare completamente le prestazioni in condizioni stazionarie. |
| Idealmente, per caratterizzare a fondo il comportamento in stato stazionario, sarebbe necessario l’input effettivo che il sistema incontrerà nelle operazioni del mondo reale. Tuttavia, negli scenari pratici, questo input specifico potrebbe non essere sempre predeterminato o conosciuto in anticipo. Di conseguenza nasce la necessità di utilizzare segnali di test standardizzati. Questi segnali di test servono come proxy per approssimare una gamma di possibili input del mondo reale, consentendo così una valutazione più solida delle prestazioni stazionarie del sistema in varie condizioni ipotetiche. |
| ## Gestione degli input sconosciuti nei sistemi di controllo |
| ### Esempi del mondo reale e la sfida degli input imprevedibili |
| Quando progettiamo sistemi di controllo, spesso affrontiamo la sfida di input sconosciuti o variabili. Esploriamolo attraverso alcuni esempi: |
| #### Esempio 1: sistema radar di tracciamento - Scenario: un sistema radar progettato per tracciare i movimenti degli aerei. - Sfida: prevedere l’esatto profilo di movimento dell’aereo è quasi impossibile. Il sistema deve essere adattabile a diverse traiettorie possibili. |
| #### Esempio 2: Controllo Numerico di Macchine Utensili - Situazione: Macchine progettate per tagliare o modellare materiali. - Complessità: alla macchina potrebbe essere richiesto di eseguire una serie di attività, dalla rastremazione al taglio di profili parabolici. Il sistema deve gestire qualsiasi forma gli venga assegnata. |
| #### Esempio 3: Impianto di riscaldamento residenziale - Condizione: variabilità delle temperature ambientali durante le stagioni. - Impatto: Questa variazione modifica sensibilmente i segnali di disturbo che il sistema deve gestire, dall’estate all’inverno. |
| In ciascuno di questi casi, l’ingresso del sistema di controllo e i segnali di disturbo che incontra non possono essere predeterminati con precisione. Questa incertezza influisce direttamente sulle prestazioni in condizioni stazionarie, che dipendono intrinsecamente dalla natura dell’input. |
| ### Affrontare input imprevedibili |
| #### Rappresentazione polinomiale degli input |
| Per superare la sfida degli input imprevedibili, una strategia consiste nel rappresentare l’input effettivo come una somma di funzioni polinomiali. Matematicamente, qualsiasi funzione complessa può essere scomposta in una serie di funzioni polinomiali più semplici. Pertanto, garantire prestazioni soddisfacenti per una serie di input polinomiali può fornire la certezza che il sistema funzionerà bene per vari input del mondo reale. |
| - Rappresentazione della funzione polinomiale: |
| Secondo la discussione precedente possiamo vedere l’input \(r(t)\) come una generica funzione polinomiale indicizzata da \(k\): |
| \[ r(t) = \frac{1}{k!} t^k \mu(t) \] |
| Qui, $ r(t) $ è una funzione polinomiale del tempo, $ k $ è l’ordine del polinomio e $ (t) $ è la funzione di passo unitario. |
| #### Ingressi polinomiali standard per prestazioni stazionarie |
| Per diversi valori di $ k $, otteniamo vari input di test standard: |
| - $ k = 0 $: $ r(t) = (t)$ diventa una funzione a passo unitario. - $ k = 1 $: $ r(t) = t (t)$ rappresenta una funzione di rampa. - $ k = 2 $: $ r(t) = t^2(t)$ forma una funzione parabolica. |
| All’aumentare di $ k $, l’input diventa più veloce, ma negli scenari pratici raramente sono necessari valori di $ k $ superiori a 2. Questo perché gli input del sistema del mondo reale generalmente non sono veloci quanto i polinomi di ordine superiore. Pertanto, nella maggior parte dei casi, è sufficiente soddisfare i criteri di prestazione per $ k = 1 $ (funzione rampa) e $ k = 2 $ (funzione parabolica). |
| #### Considerazioni pratiche sulla progettazione dei controlli |
| - Complessità e stabilità: all’aumentare dell’ordine $ k $, la progettazione del sistema di controllo diventa più impegnativa, in particolare per quanto riguarda il mantenimento della stabilità. Per $ k > 3 $ mantenere la stabilità è molto difficile. |
| - Rilevanza industriale: per molte applicazioni industriali, un valore di $ k = 1 $ è spesso sufficiente, in linea con i requisiti pratici. |
| Andando avanti, la nostra analisi si concentrerà su tre input di test fondamentali, ciascuno caratterizzato dal suo comportamento unico e dipendente dal tempo e dalla sua caratteristica natura “unitaria”, derivata dalla proprietà che i suoi derivati sono scalati all’unità: |
| 1. Funzione di passo unitario: - Rappresentazione matematica: $ r(t) = (t) $ - Caratteristiche: questa funzione rappresenta un cambiamento improvviso a $ t = 0 $, passando bruscamente da 0 a 1. È chiamata “passo unitario” perché la sua derivata, una funzione delta, raggiunge il picco all’altezza unitaria. |
| 2. Funzione Rampa Unità: - Espressione: $ r(t) = t (t) $ - Descrizione: questa funzione crescente linearmente simboleggia un ingresso di rampa che inizia a $ t = 0 $ e aumenta a una velocità costante. La designazione “unità” è dovuta al fatto che la sua derivata è costante (unità) nel tempo. |
| 3. Funzione Unità-Parabola: - Formulazione: $ r(t) = t^2 (t) $ - Spiegazione: questa funzione rappresenta una curva parabolica, che inizia da $ t = 0 $ e aumenta quadraticamente nel tempo. Il fattore \(\frac{1}{2}\) garantisce che la derivata di questa funzione, $ t (t) $, si allinei con la funzione rampa unitaria, da qui il termine ‘parabola unitaria’. |
| Ciascuno di questi input funge da segnale di test standard nell’analisi dei sistemi di controllo, fornendo una base per esaminare le risposte del sistema in diversi tipi di scenari di input. |
| ## Specifiche delle prestazioni transitorie |
| ### Approccio basato sul settore |
| Invece di fare affidamento esclusivamente su modelli matematici, un approccio basato sull’industria prevede l’esame dei sistemi di controllo del mondo reale. Eccitando questi sistemi con un ingresso a gradino standard e osservando la loro risposta, possiamo ricavare specifiche pratiche sulle prestazioni transitorie. |
| ### Osservazioni e indici di performance transitoria |
| - Risposta tipica: la risposta transitoria di un sistema di controllo pratico spesso presenta oscillazioni smorzate prima di raggiungere lo stato stazionario. |
|
| - Accettabilità delle oscillazioni: alcuni superamenti sono generalmente accettabili in scenari pratici. |
| ### Indici chiave di prestazione |
| 1. Tempo di salita ($ t_r $): è la durata necessaria affinché la risposta del sistema raggiunga inizialmente il valore finale (o il livello di stato stazionario) al 100% per la prima volta. Fornisce informazioni sulla velocità di risposta del sistema in seguito a una modifica. |
| 2. Peak Overshoot ($ M_p $): questo parametro misura il livello massimo di cui la risposta del sistema supera il suo valore finale. Se il superamento del picco rientra nei limiti accettabili, si presume generalmente che anche eventuali successive fluttuazioni di magnitudo saranno accettabili, poiché sono generalmente inferiori. |
| 3. Peak Time ($ t_p $): si riferisce al tempo trascorso dall’inizio della risposta fino al raggiungimento del suo massimo superamento. Indica la velocità con cui il sistema raggiunge il picco di risposta in seguito ad un disturbo o ad un cambiamento. |
| 4. Tempo di assestamento: è il tempo necessario affinché la risposta del sistema rimanga costantemente entro un intervallo di tolleranza specifico attorno al valore finale. L’intervallo di tolleranza, spesso fissato al 2% o al 5% del valore finale, varia in base ai requisiti di precisione dell’applicazione. Questa metrica è fondamentale per determinare la velocità con cui il sistema si stabilizza dopo fluttuazioni transitorie. |
| #### Nota aggiuntiva sulla caratterizzazione matematica del tempo di assestamento: |
| Consideriamo una funzione della forma \(e^{-t/\tau}\), che rappresenta un decadimento esponenziale. |
| Matematicamente, tale funzione si stabilizza completamente solo quando \(t\) si avvicina all’infinito (\(t \rightarrow \infty\)). |
| In altre parole, il suo tempo di assestamento teorico è infinito. Tuttavia, nell’analisi e nella progettazione pratica del sistema di controllo, definiamo un tempo di assestamento all’interno di una fascia di accettabilità pratica per riflettere condizioni operative realistiche. Questo approccio riconosce che, in pratica, un sistema è considerato “stabilizzato” quando la sua risposta è sufficientemente vicina al valore di stato stazionario, anche se non lo ha raggiunto esattamente. |
| Infine, vale la pena notare che affronteremo separatamente la precisione stazionaria-stazionaria perché non è specificata solo per un passo unitario ma anche per gli ingressi a rampa e parabolici. |
| Dati questi quattro parametri, possiamo quasi ricostruire la risposta al gradino. |
| ### Esplorazione delle dinamiche transitorie nei sistemi del secondo ordine: una simulazione interattiva |
| Possiamo vedere l’effetto della modifica di questi parametri utilizzando il seguente codice Python. |
| #### Istruzioni per l’uso: |
| 1. Slider Zeta: regolare questo cursore per modificare il rapporto di smorzamento del sistema. Un valore più basso significa meno smorzamento (più risposta oscillatoria), mentre un valore più alto significa più smorzamento (meno risposta oscillatoria). 2. Slider Omega_n: questo slider modifica la frequenza naturale del sistema. Una frequenza naturale più elevata generalmente porta ad una risposta più rapida. |
| 3. Slider del tempo della simulazione: questo cursore modifica il tempo della simulazione. |
| Con questi cursori è possibile osservare come la variazione del rapporto di smorzamento e della frequenza naturale influenzi la risposta ai transitori di un sistema stabile del secondo ordine. |
| ::: {#8ee42504 .cell} ``` {.python .cell-code} # Import necessary libraries import numpy as np import matplotlib.pyplot as plt import control |
| def find_max_consecutive_index(arr): max_consecutive_index = None consecutive_start = None |
| for i in range(len(arr) - 1): if arr[i] + 1 != arr[i + 1]: if consecutive_start is not None: max_consecutive_index = consecutive_start consecutive_start = None elif consecutive_start is None: consecutive_start = i + 1 |
| # Check if the entire array is consecutive if consecutive_start is not None: max_consecutive_index = consecutive_start |
| return max_consecutive_index if max_consecutive_index is not None else len(arr) - 1 |
| # Define a function to calculate and plot the system response with performance parameters def plot_response(zeta, omega_n, sim_time): # System parameters: zeta (damping ratio), omega_n (natural frequency) num = [omega_n**2] # Numerator (assuming unit gain) den = [1, 2 * zeta * omega_n, omega_n**2] # Denominator |
| # Create a transfer function model system = control.tf(num, den) |
| # Time parameters t = np.linspace(0, sim_time, int(sim_time*100)) # Time vector |
| # Step response t, y = control.step_response(system, t) steady_state_value = y[-1] |
| # Rise Time rise_time_indices = np.where(y >= steady_state_value)[0] rise_time = t[rise_time_indices[0]] if rise_time_indices.size else None |
| # Peak Overshoot and Peak Time peak_overshoot = np.max(y) - steady_state_value peak_time = t[np.argmax(y)] |
| # Settling Time (within 2% of steady-state value). This is found numerically. settling_time_indices = np.where(abs(y - steady_state_value) <= 0.02 * steady_state_value)[0] ts_index = find_max_consecutive_index(settling_time_indices) settling_time = t[settling_time_indices[ts_index]] if settling_time_indices.size else None |
| # Plot plt.figure(figsize=(10, 6)) plt.plot(t, y, label=‘System Response’) plt.axhline(steady_state_value, color=‘r’, linestyle=‘–’, label=‘Steady State’) # tolerange band (0.02 percent) plt.axhline(steady_state_value * 1.02, color=‘g’, linestyle=‘:’, label=‘Settling Time Bound’) plt.axhline(steady_state_value * 0.98, color=‘g’, linestyle=‘:’) |
| if rise_time: plt.axvline(rise_time, color=‘y’, linestyle=‘-’, label=f’Rise Time: {rise_time:.2f}s’) plt.axvline(peak_time, color=‘b’, linestyle=‘-’, label=f’Peak Time: {peak_time:.2f}s’) plt.scatter(peak_time, np.max(y), color=‘black’, label=f’Peak Overshoot: {peak_overshoot:.2f}’) |
| if settling_time: plt.scatter(settling_time, y[settling_time_indices[ts_index]], color=‘purple’) plt.axvline(settling_time, color=‘purple’, linestyle=‘-’, label=f’Settling Time: {settling_time:.2f}s’) |
| plt.title(‘Transient Response with Performance Parameters’) plt.xlabel(‘Time (seconds)’) plt.ylabel(‘Output’) plt.legend() plt.grid(True) plt.show() |
| # Interactive sliders from ipywidgets import interact, FloatSlider interact(plot_response, zeta=FloatSlider(value=0.3, min=0.01, max=1.0, step=0.01), omega_n=FloatSlider(value=2, min=1, max=10, step=0.1), sim_time=FloatSlider(value=10, min=1, max=50, step=1)) ``` |
| ::: {.cell-output .cell-output-display} |
{=html} <script type="application/vnd.jupyter.widget-view+json"> {"model_id":"b6369e0b55f2465e86c0dd63e6c6496c","version_major":2,"version_minor":0,"quarto_mimetype":"application/vnd.jupyter.widget-view+json"} </script> |
| ::: |
| ::: {.cell-output .cell-output-display} |