Componenti del sistema di controllo
I sistemi di controllo automatico sono onnipresenti in vari settori e applicazioni. Aiutano a mantenere le condizioni di output desiderate regolando di conseguenza l’input. Un aspetto fondamentale per comprendere questi sistemi è il concetto di sistemi analoghi e la comprensione dei componenti che compongono un sistema di controllo.
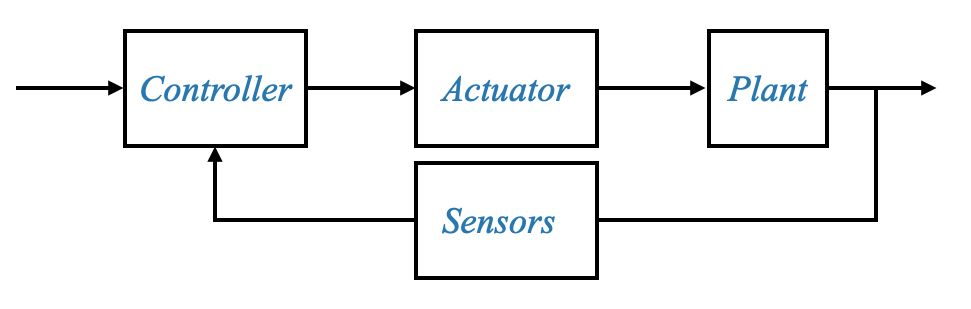
Nei sistemi di controllo automatico, l’intero processo può essere visualizzato come una sequenza di componenti interconnessi. Questa sequenza inizia con l’impianto, che è essenzialmente il sistema che intendiamo controllare. L’impianto è azionato da un attuatore e la potenza di questo attuatore è controllata dal controller, che è il cervello del nostro sistema. Il controller prende decisioni in base al feedback che riceve dai sensori che monitorano il sistema.
I sistemi di controllo sono costituiti da vari componenti che lavorano insieme per ottenere l’output desiderato.
Nella nostra discussione, ci concentreremo principalmente sui sistemi meccanici, ma, come abbiamo visto, esistono anche altri sistemi come i sistemi termici o a base liquida.
|
Componenti del Sistema di Controllo:
- Impianto: il sistema primario da controllare. Nelle nostre discussioni spesso si tratta di un sistema meccanico, ma può anche essere un sistema termico, un sistema liquido o qualsiasi altro sistema che richiede controllo.
- Attuatore: Dispositivo che aziona o controlla l’impianto. Per i sistemi meccanici, i motori sono attuatori comuni.
- Controller: il cervello del sistema. Decide come pilotare l’attuatore in base alla differenza tra l’uscita desiderata e l’uscita effettiva. Può trattarsi di un circuito amplificatore operazionale (Op-Amp) o anche di un computer digitale nei sistemi moderni.
- Sensore: dispositivo che misura la resa effettiva dell’impianto. Spesso necessita di filtri antirumore per rimuovere il rumore ad alta frequenza e di amplificatori per aumentare i segnali a livelli utilizzabili.
Il cervello del sistema di controllo, il controller, è spesso di natura elettrica. Oggi, la maggior parte dei controller sono circuiti Op-Amp (legacy) o computer digitali. In passato venivano utilizzati regolatori idraulici o pneumatici. La tendenza si sta spostando verso questi controller per la loro versatilità ed efficienza.
Il tuo ruolo:
- Progettare filtri antirumore per garantire che il rumore ad alta frequenza proveniente dai sensori non interferisca con il sistema.
- Amplificare o condizionare le uscite dei sensori per renderle compatibili con i segnali di ingresso standard o per adattarle all’hardware del controller. Ad esempio, l’uscita del sensore può essere millivolt o milliamper e richiedere un’amplificazione per utilizzarli insieme ai livelli del segnale di ingresso e con il controller.
- Progettare il controller, che è la parte più critica del sistema.
Rendiamo lo schema più preciso:
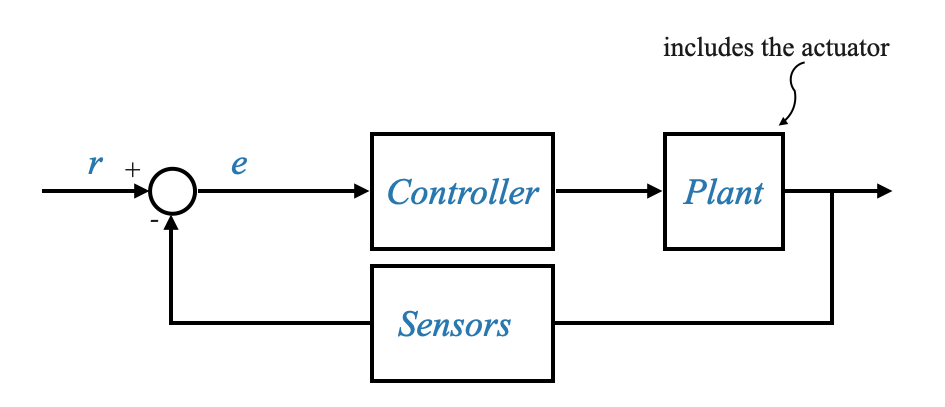
|
Il controller può rispondere al segnale di errore in vari modi. Un approccio consiste nell’amplificare l’errore, denominato controller proporzionale. Un altro metodo prevede l’utilizzo di controllori che producono un segnale basato sia sull’errore che sul suo integrale. Ciò si traduce in un segnale composto da due parti: una direttamente proporzionale all’errore e un’altra proporzionale all’errore accumulato nel tempo. Parliamo in questo caso di regolatori proporzionali e integrali.
Oltre a questi, c’è il controller proporzionale-derivativo (PD), che non solo risponde all’errore presente ma anche al tasso di variazione di questo errore. Considerando la derivata o la velocità con cui l’errore cambia, il controllore PD può anticipare gli errori futuri e agire in modo più reattivo, rendendolo particolarmente utile negli scenari in cui sono essenziali correzioni rapide.
Infine c’è il controller Proporzionale-Integrale-Derivativo (PID), che combina tutte e tre le strategie. Considera l’errore attuale (proporzionale), l’accumulo di errori passati (integrale) e il tasso di variazione dell’errore (derivativo). Utilizzando tutti e tre i componenti, il controller PID offre un approccio completo alla correzione degli errori, garantendo precisione costante, risposta rapida e anticipazione di errori futuri. Ciò rende il controller PID una delle strategie di controllo più utilizzate in vari settori grazie alla sua adattabilità ed efficienza in diversi scenari di controllo.
- Regolatore proporzionale (P): \[ u(t) = K_p \cdot e(t) \]
Dove: - $ u(t) $ è l’uscita di controllo. - $ K_p $ è il guadagno proporzionale. - $ e(t) $ è il segnale di errore.
- Regolatore Proporzionale-Integrale (PI): \[ u(t) = K_p \cdot e(t) + K_i \int e(t) \, dt \]
Dove: - $ K_i $ è il guadagno integrale.
- Regolatore proporzionale-derivato (PD):
\[ u(t) = K_p \cdot e(t) + K_d \frac{d e(t)}{dt} \]
Dove: - $ K_d $ è il guadagno derivato.
- Regolatore proporzionale-integrale-derivativo (PID):
\[ u(t) = K_p \cdot e(t) + K_i \int e(t) \, dt + K_d \frac{d e(t)}{dt} \]
In queste equazioni: - $ e(t) $ rappresenta il segnale di errore, ovvero la differenza tra il setpoint e la variabile di processo (o l’uscita misurata). - I guadagni $ K_p $, $ K_i $ e $ K_d $ determinano rispettivamente la forza della risposta del controllore all’errore, il suo accumulo e il suo tasso di variazione. La regolazione di questi guadagni consente di ottimizzare le prestazioni del controller per adattarle ad applicazioni specifiche.
Questi possono essere facilmente implementati come controller analogici utilizzando amplificatori operazionali.
Controller analogici
Gli amplificatori operazionali (Op-Amp) sono componenti cruciali nei sistemi di controllo. Possono fungere da amplificatori, integratori o differenziatori, a seconda della loro configurazione.
- Regolatore Proporzionale (P):
Circuito:
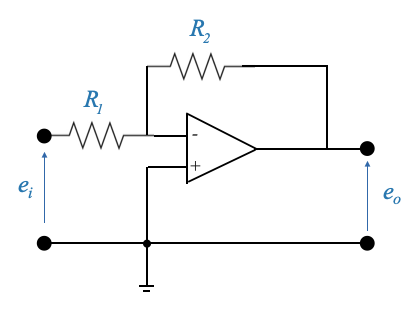
Funzione di trasferimento:
\[ \frac{E_0(s)}{E_i(s)}=-\frac{R2}{R1} \]
- Notare che con due circuiti in serie si può eliminare il segno meno.
- Regolatore proporzionale-integrale (PI):
Circuito:
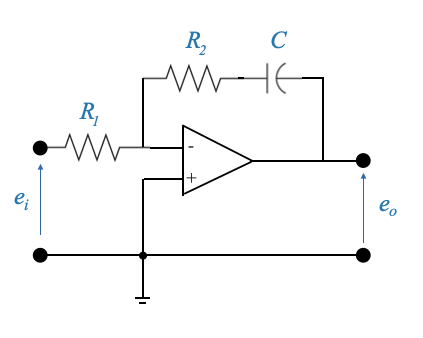
Funzione di trasferimento:
\[ \frac{E_0(s)}{E_i(s)}=-\frac{R_2+\frac{1}{sC}}{R_1} = -\frac{R_2}{R_1} - \frac{1}{R_1C }\frac{1}{s} \]
che possiamo scriverlo come:
\[ e_0(t) = -\frac{R_2}{R_1}e_i(t) - \frac{1}{R_1C}\int_{0}^{t}e_i(\tau)d\tau \]
- Controllore Proporzionale-Derivativo (PD):
Circuito:
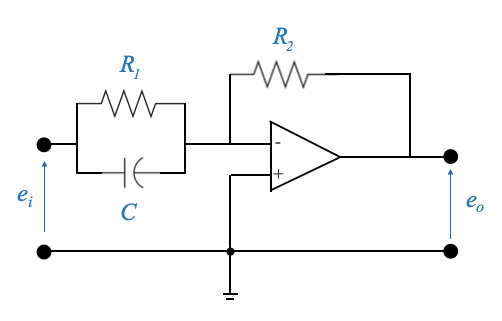
Funzione di trasferimento:
\[ \frac{E_0(s)}{E_i(s)}=\frac{\frac{R_2}{R_1\frac{1}{sC}}}{R_1+\frac{1}{sC}} \]
e con semplici manipolazioni possiamo ottenere la struttura standard.
- Regolatore proporzionale-integrale-derivativo (PID):
Circuito:
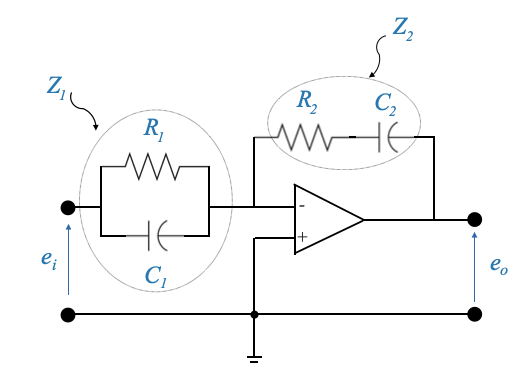
Funzione di trasferimento:
\[ \frac{E_0(s)}{E_i(s)} = -\frac{Z_2(s)}{Z_1(s)} \]