import numpy as np
import matplotlib.pyplot as plt
import control

Standard Feedback loop

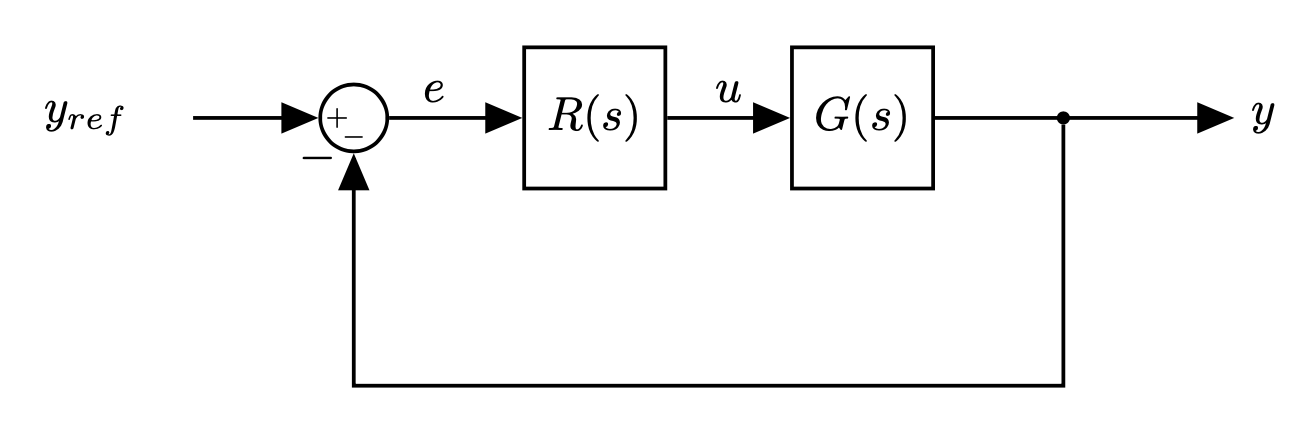Controller $R(s)$:

• Converts the error term into an actuator command
• We are free to choose any control scheme we like.
• As long as the closed loop performance of the system meets our requirements

Note: controller = compensator

• Lead and lag compensators are used quite extensively in control.
• A lead compensator can increase the stability or speed of reponse of a system;
• A lag compensator can reduce (but not eliminate) the steady-state error.
• Depending on the effect desired, one or more lead and lag compensators may be used in various combinations.
• Lead, lag, and lead/lag compensators are usually designed for a system in transfer function form.

Phase Lead

• What is phase lead

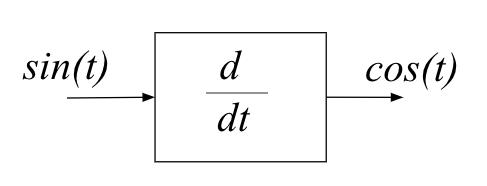t = np.arange(0, 10, 0.1)
plt.plot(t, np.sin(t), color='r', label='sin');
plt.plot(t, np.cos(t), color='b', label='cos');
plt.legend();
plt.grid()

• The $cos$ signal is ahead of the $sin$ signal by $90$ deg
• The output leads the input by 90 deg

We can plot the Bode plots:

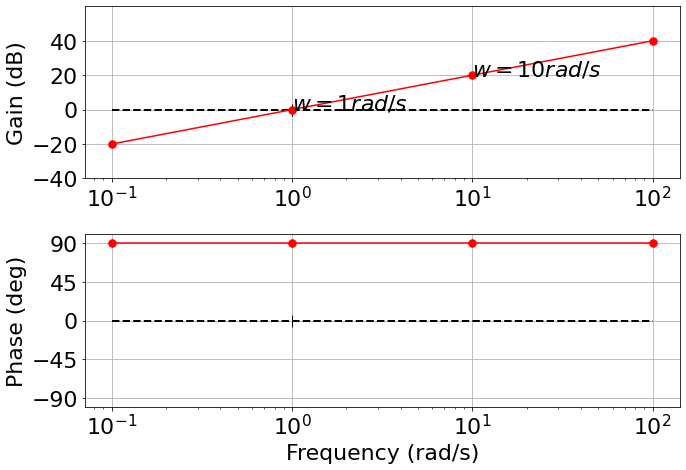• Differentiation gives positive phase

• Integration gives negative phase (Mirrors the derivative plot)

• A zero in a transfer function adds phase

• A pole in a transfer function subtracts phase

• Lead compensator: adds phase (at least in some frequency range of interest)

• Lag compensator: subtracts phase (at least in some frequency range of interest)

Equations

Lead compensator

$$ R(s) = \frac{\frac{s}{w_z}+1}{\frac{s}{w_p}+1} = \frac{w_p}{w_z}\frac{s + w_z}{s + w_p} $$

• one real pole and one real zero
• $w_z < w_p$
• $K=\frac{w_p}{w_z}$ (gain)
• We can take care of the gain easily (e.g., using the root locus method)

Lag compensator

$$ R(s) = \frac{\frac{s}{w_z}+1}{\frac{s}{w_p}+1} = \frac{w_p}{w_z}\frac{s + w_z}{s + w_p} $$

• one real pole and one real zero
• $w_z > w_p$
• $K=\frac{w_p}{w_z}$ (gain)

Bode plot: Lead Compensator

$$ R(s) = \frac{w_p}{s + w_p}\frac{s + w_z}{w_z} $$

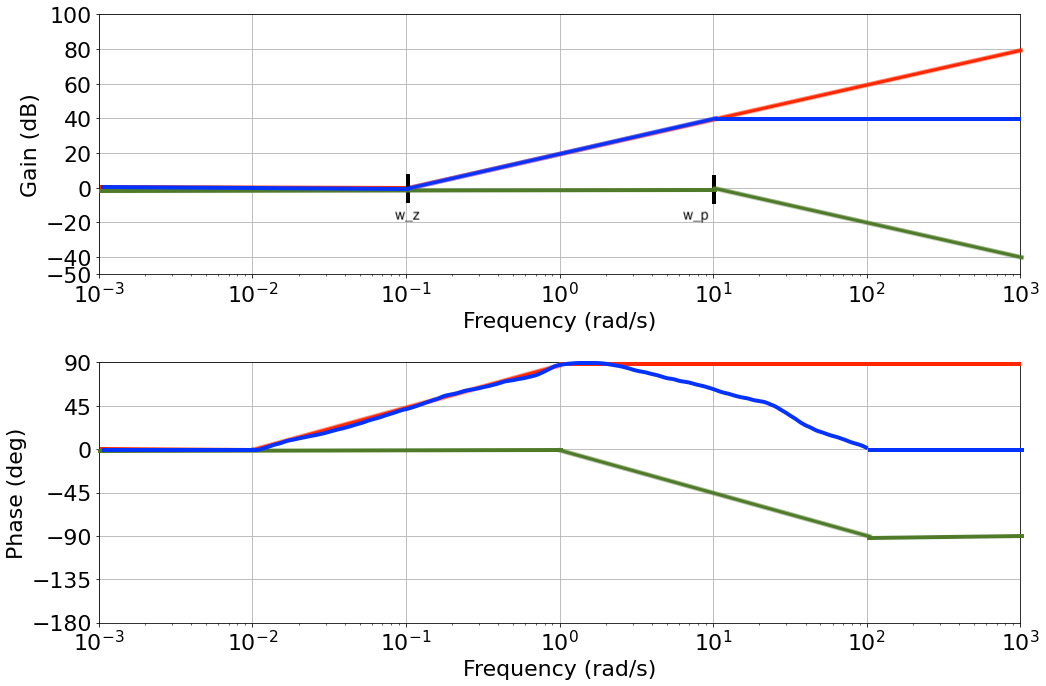
Let's look at the zero-pole contribution separately:

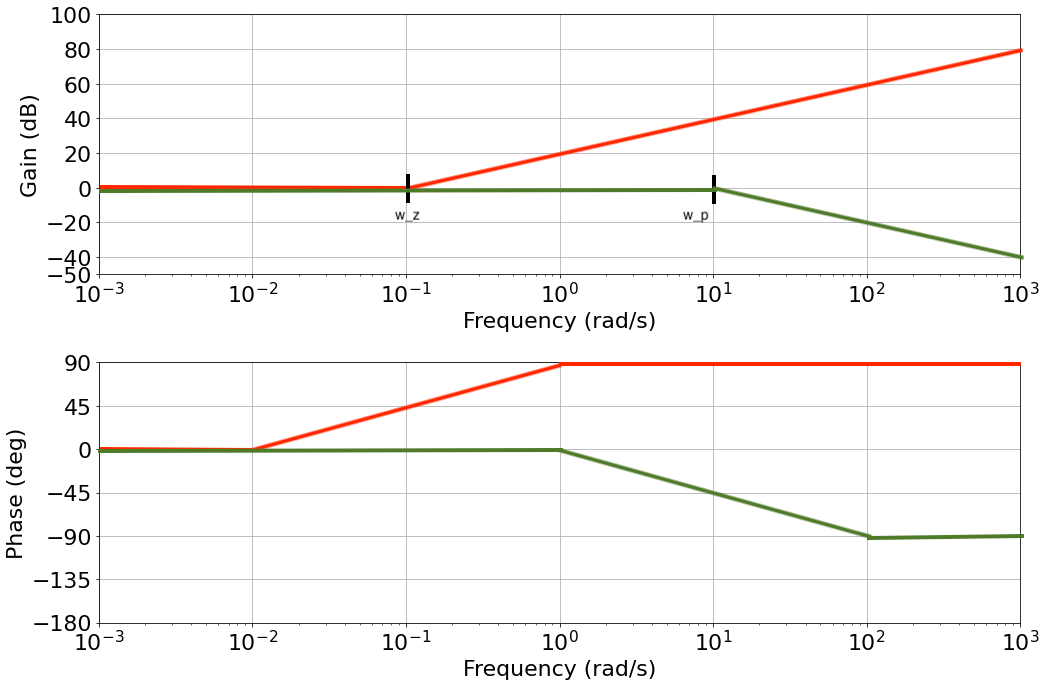• The zero adds 90 deg and amplifies high frequencies
• The pole subtracts 90 deg and attenuates high frequencies

• Multiplying the two T.F. together means adding everything together on the Bode plot
• Lead/Lag compensator:
  • Behaves like a real zero early on, at low frequency
  • Until the real pole pulls it back at high frequency
  • See blue line for its approximate representation

Note:

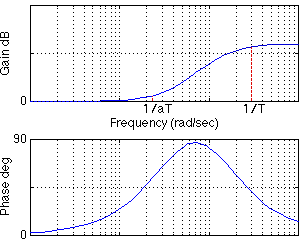
• A lead compensator increases the gain at high frequency (but less than a real zero would do)
• This means that it is less noisy than a derivative controller on its own
• A lead compensator adds phase between the two corner frequencies and no phase outside
• Moving the two frequency means we can change where we add our phase

Example

Let's see an example:

w_z = 1
w_p = 10

s = control.tf([1, 0], [1])

R_s = w_p/(s+w_p)*(s+w_z/w_z)

We can plot the zero (blue) and the pole (orange) parts together with the combined Bode plot (green):

fig, axs = plt.subplots(1, figsize=(10,5))

# zero (blue)
control.bode_plot((s+w_z)/w_z, dB=True, omega_limits = [0.1, 100], wrap_phase =True);
# pole (orange)
control.bode_plot(w_p/(s+w_p), dB=True, omega_limits = [0.1, 100], wrap_phase =True);

# compensator (green)
control.bode_plot(R_s, dB=True, omega_limits = [0.1, 100], wrap_phase =True);

# Note: If wrap_phase is True the phase will be restricted to the range [-180, 180) (or [-\pi, \pi) radians)

• What happens when we move the zero closer to the pole?

w_z = 5
w_p = 10

fig, axs = plt.subplots(1, figsize=(10,5))

# zero (blue)
control.bode_plot((s+w_z)/w_z, dB=True, omega_limits = [0.1, 100], wrap_phase =True);
# pole (orange)
control.bode_plot(w_p/(s+w_p), dB=True, omega_limits = [0.1, 100], wrap_phase =True);

# compensator transfer function (green)
R_s = w_p/(s+w_p)*(s+w_z)/w_z
control.bode_plot(R_s, dB=True, omega_limits = [0.1, 100], wrap_phase =True);

• Still a phase lead is present, but much smaller
• What happens if the zero is right on top of the pole?

• if $w_p$ < $w_z$ we obtain a lag compensator

w_z = 50
w_p = 10

fig, axs = plt.subplots(1, figsize=(10,5))
# zero
control.bode_plot((s+w_z)/w_z, dB=True, omega_limits = [1, 1000], wrap_phase =True);
# pole
control.bode_plot(w_p/(s+w_p), dB=True, omega_limits = [1, 1000], wrap_phase =True);

# compensator transfer function
R_s = w_p/(s+w_p)*(s+w_z)/w_z
control.bode_plot(R_s, dB=True, omega_limits = [1, 1000], wrap_phase =True);

• The zero affects the system at higher frequency
• The system behaves like a real pole at lower frequency
• Until the zero comes into effect and "cancels" the pole at higher frequency
• This add lag to the system

Note: The sama transfer function structure can produce phase lead or lag, adjusting the relative position of the pole and the zero

Lead/Lag compensators

• Design a compensator that uses both a lead and a lag compensator:

$$ R(s) = \frac{\frac{s}{w_z}+1}{\frac{s}{w_p}+1} \frac{\frac{s}{w_{z1}}+1}{\frac{s}{w_{p1}}+1} = \frac{w_p}{w_z}\frac{s + w_z}{s + w_p}\frac{w_{p1}}{w_{z1}}\frac{s + w_{z1}}{s + w_{p1}} $$

w_z = .5
w_p = 1

R_Lead = w_p/(s+w_p)*(s+w_z)/w_z

# Lag compensator
w_z1 = 15
w_p1 = 5

R_Lag = w_p1/(s+w_p1)*(s+w_z1)/w_z1

Plot the pole zero map for the Lead compensator:

control.pzmap(R_Lead);

Plot the pole zero map for the Lag compensator:

control.pzmap(R_Lag);

We construct the Lead-Lag compensator:

R_LL = R_Lead*R_Lag

And we can plot the Bode Plot to see what the phase does:

fig, axs = plt.subplots(1, figsize=(10,5))
control.bode_plot(R_LL, dB=True, omega_limits = [.01, 1000], wrap_phase =True);

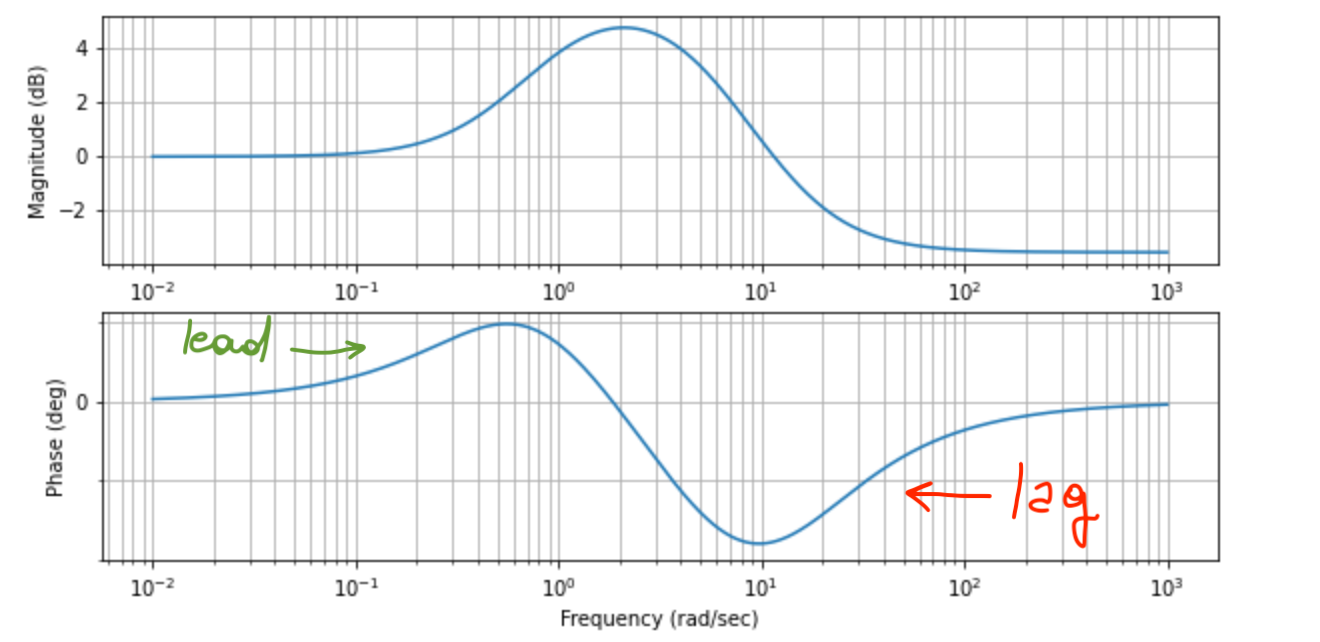• This compensator is leading at low frequency, and lagging at higher frequency

Designing a Lead Compensator with the Root Locus

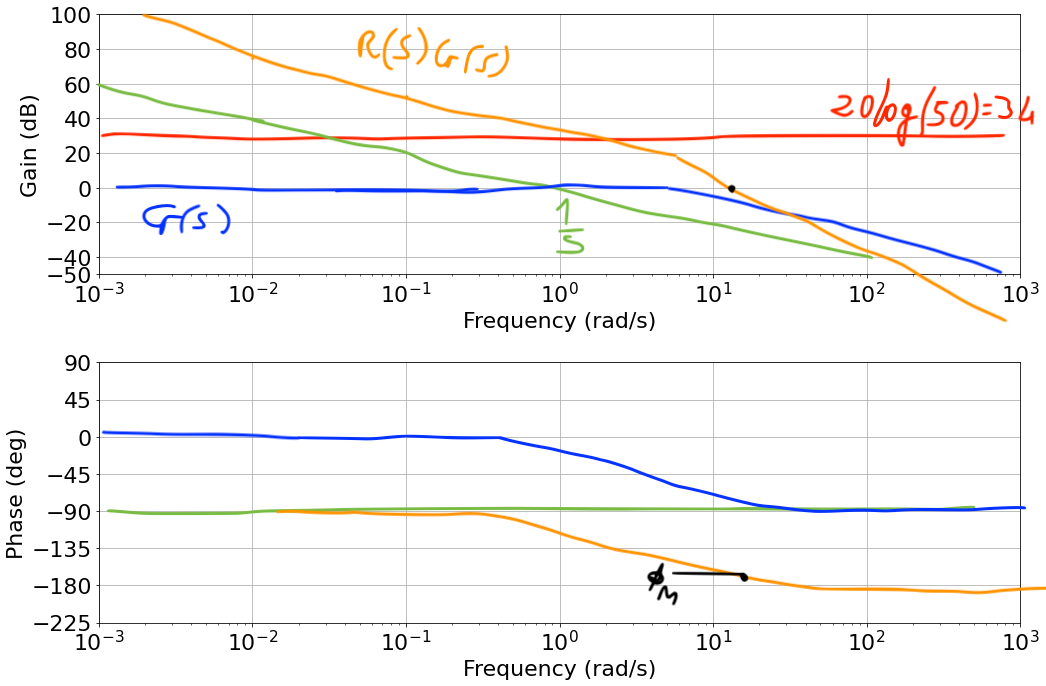
• Let's consider our control loop again:

• We have a model of our plant $G(s)$

  • we are given a transfer function
  • we have identified the model

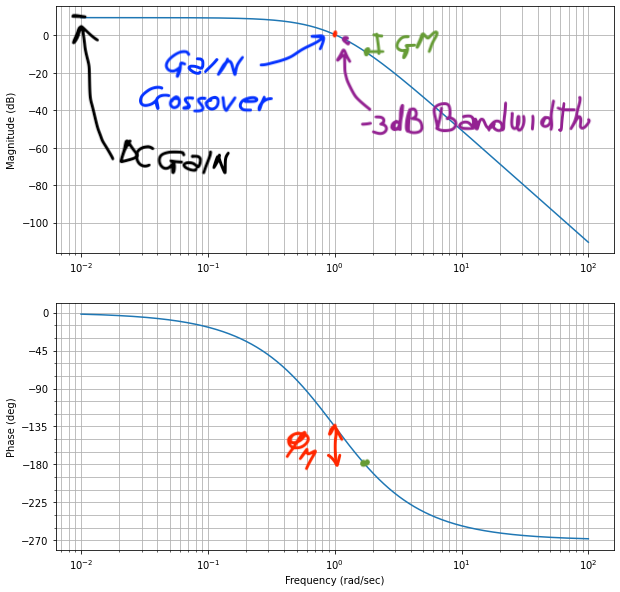
• Design requirements - performance goal:

  • Stability
  • Rise time
  • Settling time
  • Max Overshoot
  • Damping ratio
  • Gain/Phase margin

• $G(s)$ alone does not meet our requirements

• We need to design the controller $R(s)$

• How do we choose $R(s)$?

Let's consider:

$$ G(s) = \frac{1}{(s+2)(s+4)} $$

• What is the Root Locus of $G(s)$?

s = control.tf([1, 0],[1])

G_s = 1/((s+2)*(s+4))

fig, axs = plt.subplots(1, figsize=(10,5))
control.rlocus(G_s);

• What if we had a Lead compensator?
• How does the root locus change?

Let's choose, arbitrarily, a Lead compensator ($w_z < w_p$):

$$ R(s) = \frac{(s+5)}{(s+6)} $$

Let's see how it looks like with Python:

We define the controller:

R_s = (s+5)/(s+6)

Plot the Root Locus:

fig, axs = plt.subplots(1, figsize=(10,5))
control.rlocus(G_s*R_s);

With a lead compensator:

• We have moved the asynmptotes further into the left half plane
• Increasing the gain $K$ the close loop poles would be more to the left: we have added stability to the system

How does this help us?

• When we use the root locus method we typically know where we would like our dominant closed loop poles to be so that we meet our requirements
• With the root locus method, we first convert our requirements into pole locations

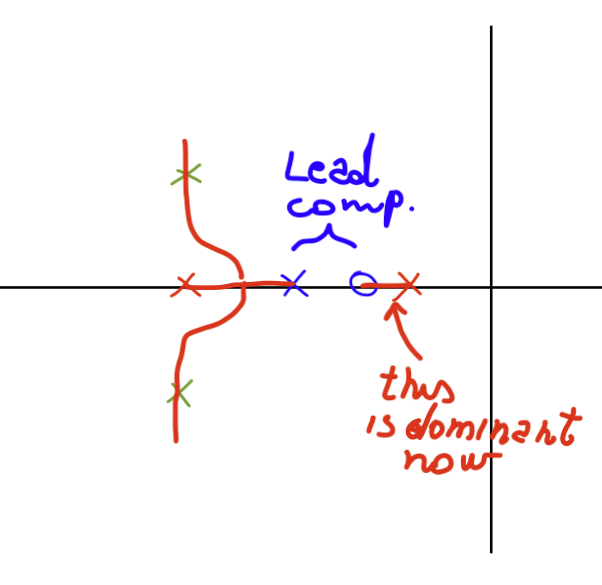
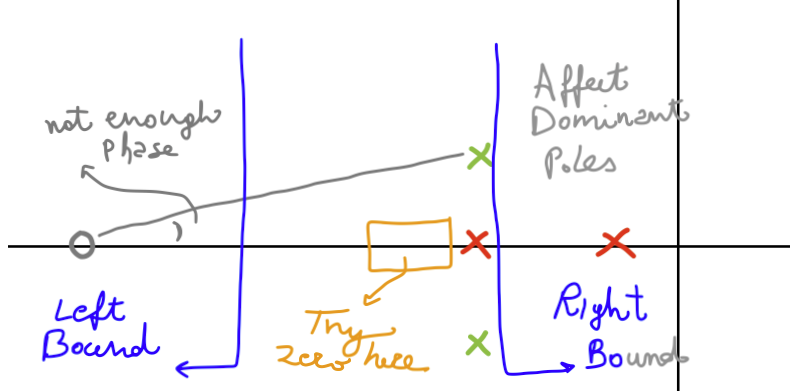
• We need a lead compensator if we need to move our poles to the left of where our current (uncompensated) poles are
• We need a lag compensator if we need to move our poles to the right of where our current (uncompensated) poles are
• If the root locus already goes through the desired locations, we only need to choose the correct gain
  • Note: we could still have a steady state error problem, but we know how to fix this already

• Given desired poles, solving for the compensator becomes a trigonometry problem:

• To be part of the Root Locus: $\sum{\angle Poles} - \sum{\angle Zeros} = 180^o$

For example, for our system we saw that the root locus is:

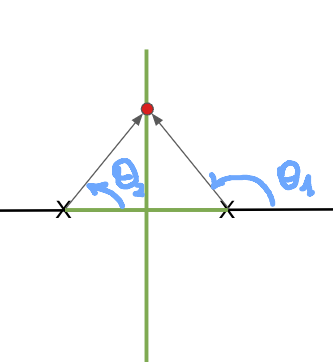• There are no zeros (so we do not need to subtract)
• The sum of $\theta_1+\theta_2$=180 because that point is part of the root locus

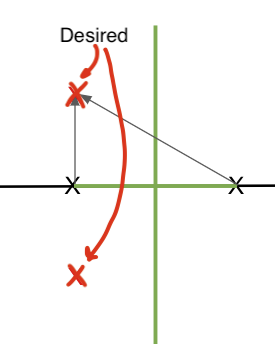
Given our system: $$ G(s) = \frac{1}{(s+2)(s+4)} $$

If we want poles:

$$s_d = -4 \pm 2j$$

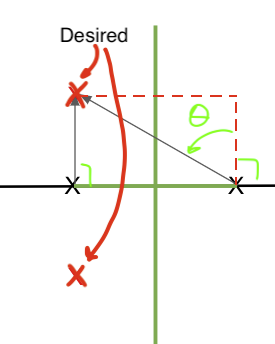And if we sum up all the angles: $90+(90+\theta)$ = $90+(90+45)$ = 225

• since $\theta = \tan^{-1}(2/2) = \tan^{-1}(1) = 45$

And of course, this is not on the Root Locus.

• To have it on the Root Locus, we need to remove 45 deg of phase
• Using a phase lead compensator we can do it adding a single pole and a single zero:

$$ 225 + (\theta_p - \theta_z) = 180 $$

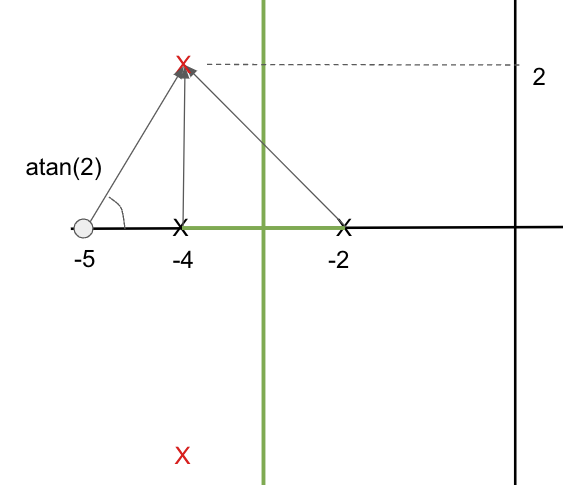
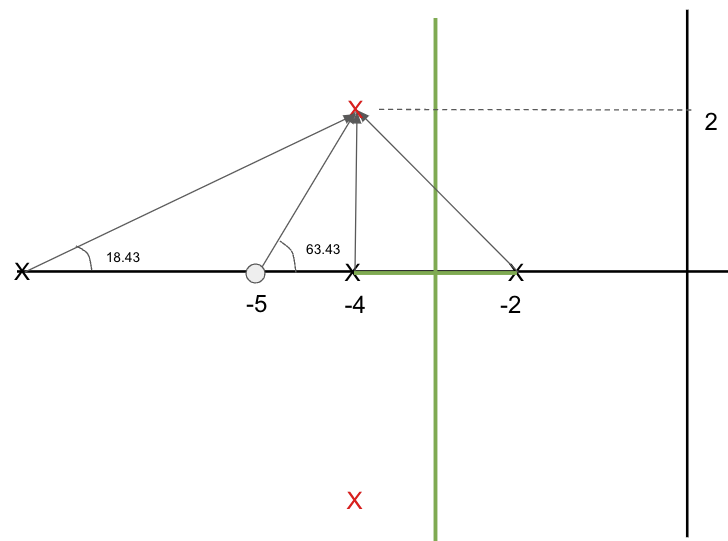
• $(\theta_p - \theta_z)$ is our lead compensator

• If we pick a zeros at -5
  • $\theta_z= 63.43 ^o$
• The pole must go into one specific location:
  • $\theta_p=180-225+63.43=18.43$

The compensator for this particular problem is:

$$ R(s) = \frac{s+5}{s+10.015} $$

%matplotlib notebook
R_s = (s+5)/(s+10.015)
fig, axs = plt.subplots(1, figsize=(7,7))
control.rlocus(G_s*R_s);

One more step:

• We need to calculate the gain that moves the poles in closed loop where we want them

$$ \frac{KG(s)R(s)}{1+KG(s)R(s)} $$

We can then find:

$$ K = \frac{-1}{1+G(s)R(s)}\Big|_{s=-4 + 2 j} \approx 16 $$

Choosing the first zero

• No hard and fast rule
• We need to have enough negative angle to bring the sum to 180 deg
• Pay attention not to interfere with your dominat poles
  • For example, if you had:

We can then sketch bounds:

</tr> </table>

Rule fo thumb: place your zero at or closely to the left of the second real axis open loop pole

• Does not guarantee that overshoot requirements will be met
• Trial and error might be needed
• With higher order systems, might be difficult to predict where other non-dominant poles go: we must avoid making them unstable
• Faster responding system means responding to noise as well.

---

Designing a Lag Compensator with Root Locus

$$ R(s) = \frac{\frac{s}{w_z}+1}{\frac{s}{w_p}+1} = \frac{w_p}{w_z}\frac{s + w_z}{s + w_p} $$

• one real pole and one real zero
• $w_z > w_p$
• $K=\frac{w_p}{w_z}$ (gain)

We can re-write the above equation as:

$$ R(s) = \frac{\tau_z s + 1}{\tau_p s + 1} $$

• The transfer function has the same structure
• We can use the same design technique that we saw for the Lead Compensators

• With a Phase Lag compensator we can move our dominant poles closer to the imaginary axis
• This is however not the main reason Lag Compensators
• Lag Compensators are useful to address steady state errors
  • e.g., error to the step input
  • improve steady state errors, without changing the position of the dominant poles (they are already where we need them)
  • this means we do not want shape the root locus very much

How does a lag compensator reduce $E_{ss}$

Where: $$ G(S) = \frac{N(s)}{D(s)} $$

and our Lag compensator is:

$$ R(s) = \frac{s-z}{s-p} $$

and the input is $U(s)$.

The steady state error for the uncompensated system is:

$$ E_{ss} = \lim_{s\rightarrow0} s \cdot \frac{U(s)}{1+\frac{N(s)}{D(s)}} $$

For a step input: $U(s)=\frac{1}{s}$

$$ \Rightarrow E_{ss} = \lim_{s\rightarrow0} s \cdot \frac{U(s)}{1+\frac{N(s)}{D(s)}} = \frac{D(0)}{D(0)+N(0)} $$

The steady state error for the compensated system is:

$$ E_{ss} = \lim_{s\rightarrow0} s \cdot \frac{U(s)}{1+\frac{N(s)(s-z)}{D(s)(s-p)}} $$

For a step input: $U(s)=\frac{1}{s}$

$$ \Rightarrow E_{ss,c} \lim_{s\rightarrow0} s \cdot \frac{U(s)}{1+\frac{N(s)(s-z)}{D(s)(s-p)}} = \frac{D(s)(s-p)}{D(s)(s-p)+N(s)(s-z)}\Big|_{s\rightarrow0} = \frac{D(0)p}{D(0)p+N(0)z} $$$$ \frac{z}{p} = \frac{D(0)-E_{ss,c}D(0)}{E_{ss,c}N(0)} $$

• We can choose $E_{ss,c}$ and have the corresponding $\frac{z}{p}$
• To have $E_{ss,c}=0$, $\frac{z}{p} \rightarrow \infty$
• We can only reduce the steady state error and not eliminate it. We need to change the system type to eliminate it

Example

$$ G(s) = \frac{5s^2+6s+2}{4s^2+s+3} $$

• Goal: reduce steady state error $E_{ss, c}=0.1$

$$ \frac{z}{p} = \frac{D(0)-E_{ss,c}D(0)}{E_{ss,c}N(s)} = \frac{3-E_{ss, c}\cdot 3}{E_{ss, c}\cdot2} = \frac{3-0.1\cdot3}{0.1\cdot2} = 13.5 $$

• We know the zero/pole ratio
• Where do we place them?
• E.g., $z=-0.1$, $p=-1.35$ or $z=1$, $p=13.5$ would work

Remember that the Root Locus is where the angles of poles (+) and zeros (-) add to 180 degrees

• We do not want to move the location of our roots too much when using a Lag compensator
• The the angle of the poles and zeros of the compensator should be very small (no Root Locus shaping):

$$ \theta_p - \theta_z \approx 0 $$

• Meeting the condition above while keeping the desired $\frac{z}{p}$ is much easier if we place the zero and pole very close to the imaginary axis
• Practical constraints means you cannot move them too close (resistors and capacitors limits)

Rule of thumb: the location of the zero is approximately 50 times closer to the imaginary axis as the closer dominant pole

E.g.,

• dominant poles at $-1\pm \text{Imag} j$
• zero at $-1/50=0.02$
• pole at $\Big(\frac{z}{p}\Big)_{des} = \frac{0.02}{p}$

Example

$$ G(s) = \frac{1}{(s+1)(s+3)} $$

With a Lead compensator to meet stability and rise time requirements $$ R(s) = \frac{16(s+4)}{(s+9)} $$

In this case: $$ E_{ss} = \frac{D(0)}{D(0)+N(0)} = \frac{9\cdot3\cdot1}{9\cdot3\cdot1+16\cdot4}\approx 0.3 $$

Requirement: $E_{ss} =0.1$

$$ \frac{z}{p} = \frac{D(0) -E_{ss} D(0)}{E_{ss} N(0)} = \frac{9\cdot3\cdot1 - 0.1\cdot9\cdot3\cdot1}{0.1\cdot16\cdot4} \approx 3.8 $$

Dominant poles: $s_{1,2} = -3\pm-2j$

• The zero goes to $\frac{-3}{50} = -0.06$
• The Pole goes to $3.8 = \frac{-0.06}{p} \Rightarrow p = -0.6/3.8 = -0.016$

Lag compensator: $$ R(s) = \frac{s+0.06}{s+0.016} $$

• We can have the Lag compensator in series with a Lead compensator

Exercise:

• Plot the step response and the impulse respose of the uncompensated and compensated system

s = control.tf([1, 0],[1])

sys_u = 1/((s+1)*(s+3))*(16*(s+4)/(s+9))
print('sys_u', sys_u)

sys_c = 1/((s+1)*(s+3))*(16*(s+4)/(s+9))*(s+0.06)/(s+0.016)
print('sys_c', sys_c)

sys_u 
       16 s + 64
------------------------
s^3 + 13 s^2 + 39 s + 27

sys_c 
           16 s^2 + 64.96 s + 3.84
---------------------------------------------
s^4 + 13.02 s^3 + 39.21 s^2 + 27.62 s + 0.432

t_u, yout_u = control.step_response(control.feedback(sys_u, 1), T=100)
t_c, yout_c = control.step_response(control.feedback(sys_c, 1), T=100)

fig, ax = plt.subplots(1, figsize=(10,7))

plt.plot(t_u, yout_u, color='b', label='uncompensated');
plt.plot(t_c, yout_c, color='r', label='compensated');
plt.grid();
plt.legend();
plt.yticks(np.arange(0, 1, 0.1));

• As expected: the uncompensated system has $E_{ss} = 0.3$
• The compensated system has $E_{ss} = 0.1$
• Settling time does not change very much, as desired

We can see this better looking at the impulse response

t_u, yout_u = control.impulse_response(control.feedback(sys_u, 1), T=3)
t_c, yout_c = control.impulse_response(control.feedback(sys_c, 1), T=3)

fig, ax = plt.subplots(1, figsize=(10,7))

plt.plot(t_u, yout_u, color='b', label='uncompensated');
plt.plot(t_c, yout_c, color='r', label='compensated');
plt.grid();
plt.legend();
plt.yticks(np.arange(0, 1.5, 0.1));

• This confirmes that we did not change the position of the dominant poles very much

---

Designing a Lead Compensator with the Bode Plot

• Let's consider our control loop again:

• Compensator: Lead compensator, so we need to select one pole and one zero

• First: Convert requirements to frequency domain requirements if needed
  • Gain/Phase margin
  • Bandwidth
  • Gain crossover frequency
  • Zero-frequency magnitude or DC Gain
  • Steady-state error

A phase-lead compensator can also be designed using a frequency response approach. A lead compensator in frequency response form is given by the following transfer function:

$$ Lead(s) = \frac{a\tau s + 1}{\tau s + 1} $$

with $a>1$ (when $a<1$ we would have a lag compensator).

Note that the previous expression is equivalent to the form (which we used for the Root Locus):

$$ Lead(s) = K\frac{s + w_z}{s + w_p} $$

when $w_p =\frac{1}{\tau}$, $w_z = \frac{1}{a\tau}$, and $K = a$.

In frequency response design, the phase-lead compensator adds positive phase to the system over the frequency range $\frac{1}{a\tau}$ to $\frac{1}{\tau}$.

And a Bode plot of a phase-lead compensator $Lead(s)$ has the following form:

• The two corner frequencies are at $\frac{1}{a\tau}$ and $\frac{1}{\tau}$

• Note the positive phase that is added to the system between these two frequencies.

• Depending on the value of $a$, the maximum added phase can be up to 90 degrees

• If you need more than 90 degrees of phase, two lead compensators in series can be employed.

Example

$$ G(s) = \frac{1}{0.2s+1} $$

System requirements

• Steady state error < 0.02 to a unit ramp input
• Phase margin $> 48$ deg

1. For a ramp unit (assuming a stable system):
   • we need at least a type 1 system to have a finite error (single pole at the origin)
   • we need at least a type 2 system to have a zero error

Note we cannot meet our requirements with a lead compensator alone. It does not have a pole at the origin

Our controller needs to have this structure to start from $$ R(s) = K\frac{1}{s} $$

and now we can add the lead compensator to deal with the phase margin.

• It is always better to start from the type of the system: adding a pole at the origin will affect your phase.

• Given that a single pole at the origin is enough, we will not add a second one

  • Adds complexity
  • Might reduce stability
  • Do not overdesign!

1. Choose the gain to meet $e_{ss} < 0.02$

For an input $U(s)$:

$$ e_{ss} = \lim_{s\rightarrow0}sE(s) = s \frac{1}{1+G_F(s)}U(s) $$

where, in this case:

$$ G_F(s) = G(s)K\frac{1}{s} $$$$ Ramp = \frac{1}{s^2} $$

If we plug in the numbers:

$$ e_{ss} = \lim_{s\rightarrow0}sE(s) = s \frac{1}{s^2}\frac{0.2s^2+s}{0.2s^2+s+K+1} < 0.02 \Rightarrow K > 49 $$

We can then choose:

$$ R(s) = 50\frac{1}{s} $$

Let's now draw the Bode plot:

• Bring the system in the Bode form
• Sketch the Bode Diagram for each individual part
• Add them all up

Let's check it with Python

s = control.tf([1, 0], [1])
G_s = 1/(0.2*s+1)
R_s = 50/s

fig, ax = plt.subplots(1, figsize=(10,7))
control.bode_plot(G_s*R_s, dB=True);

[gm, pm, _, pm_f] = control.margin(G_s*R_s)

print('Phase margin: deg', pm, 'at rad/s', pm_f)

Phase margin: deg 17.964235916371393 at rad/s 15.421164188583809

We do not respect our phase margin requirement $18<48$

• A lead compensator adds phase for a specific frequency range
• We also add gain, which means we move the crossover frequency to higher frequency

• To determin how much phase let's look at the lead compensator equations, which we can re-write in this form to highlight the relative relationship between the pole and the zero:

$$ Lead(s) = \frac{a\tau s + 1}{\tau s + 1} $$

• In this form, the steady state gain is 1 (0 dB). Does not affect the steady state we already determined.
• $a > 1$ to be a lead compensator
• $a < 1$ is a lag compensator

From the equation above it is easy to verfy that the following equations can be used to determine significant points of the response:

Upper cutoff frequency $$ w_u = \frac{1}{a\tau} $$

• gain starts to increase

Lower cutoff frequency

$$ w_l = \frac{1}{\tau} $$

• gain starts to flatten out

Max phase (obtained at the center frequency $w_m$)

$$ \Phi_{max} = \sin^{-1} \Big( \frac{a-1}{a+1} \Big) $$

Freq at Max phase $$ w_{m} = \frac{1}{\tau\sqrt{a}} $$

Gain at Max phase $$ Gain_{m} = \sqrt{a} $$

Choosing $a$ and $\tau$:

1. Choose the maximum phase you would like to add $\Phi_{max}$ and solve for $a$
2. Choose the frequency $w_{m}$ where you would like to add $\Phi_{max}$ and solve for $\tau$

• We would get a lower phase increase
• Trial and error is an option
  • Add a safety factor (e.g., 15 deg)

Let's go back to our design

• We need 30 deg more at 15 rad/s (from 18 to 38)
• We add some safety factor:

$$ \Phi_{max} = \sin^{-1} \Big( \frac{a-1}{a+1} \Big) = 37 \Rightarrow a=4 $$

Freq at Max phase $$ w_{m} = \frac{1}{\tau\sqrt{a}} = 22.2 rad/s \Rightarrow \tau=0.022 $$

Final controller:

$$ R(s) = 50\frac{1}{s}\frac{0.088s+1}{0.022s+1} $$

And we should verify that we obtain the desired phase margin plotting the Bode plot.

Let's plot the Bode plots for

• the initial controller (in blue) $$ R(s) = G(s)\frac{50}{s} $$

• the final lead compensator (in orange) $$ R(s) = 50\frac{1}{s}\frac{0.088s+1}{0.022s+1} $$

s = control.tf([1, 0], [1])
G_s = 1/(0.2*s+1)
R_s = 50/s*(0.088*s+1)/(0.022*s+1)

fig, ax = plt.subplots(1, figsize=(10,7))
control.bode_plot(G_s*50/s, dB=True, wrap_phase=True, omega_limits=[0.1, 1000]);

control.bode_plot(G_s*R_s, dB=True, margins=True, wrap_phase=True, omega_limits=[0.1, 1000]);

• The gain plot did not change too much
• We can see the lead compensator as a delta that we sum to the uncompensated Bode plot

• We can only add up to $\Phi_{max}= 90$ deg (there is only one zero)

• In practice: $\Phi_{max} < 55$ deg

• More phase lead needed means two lead compensators in series

---

Designing a Lag Compensator with the Bode Plot

• Let's consider our control loop again:

$$ G(s) = \frac{1}{0.2s+1} $$

System requirements

• Steady state error < 0.02 to a unit ramp input
• Phase margin $> 48$ deg

When we designed the Lead compensator using the Bode plots:

• We saw we need a type 1 system at least, and then we chose the gain $K$ to meet our steady state error requirement

We designed an initial controller:

$$ R(s) = \frac{50}{s} $$

• Achieves requirement 1, but not 2

s = control.tf([1, 0], [1])
G_s = 1/(0.2*s+1)
R_s = 50/s

fig, ax = plt.subplots(1, figsize=(10,7))

control.bode_plot(G_s*R_s, dB=True, margins=True, wrap_phase=True, omega_limits=[0.1, 1000]);

• Before, we used a Lead compensator to meet our phase requirement, with the final controller that was:

$$ R_s = \frac{50}{s}\frac{(0.088s+1)}{(0.022*s+1)} $$

• We could use a Lag compensator to meet our phase margin requirement

• But with the Lag compensator we meet the requirement changing the gain crossover frequency

• Note that we want to still retain the performance we obtained before with the partially compensated system (i.e., when we were using the controller $\frac{50}{s}$. This means that we do not want to change the DC gain because that has been set to achieve the steady state requirements

Let's consider a typical Lag Compensator Bode Plot.

And to do so, we consider:

$$ R_{lag}(s) = \frac{2s+1}{4s+1} $$

fig, ax = plt.subplots(1, figsize=(10,7))
control.bode_plot((2*s+1)/(4*s+1), dB=True, wrap_phase=True);

• A low frequency, the gain is 1 (0 dB)
• Useful because we do not want to change our DC gain
• At high frequency, the magnitude is 1/2 or -6dB (for this specific choice of zero/pole)

• We want to leverage the high frequency attentuation with a relative flat frequency shift to move the crossover frequency and the 0dB DC gain at low frequency not to impact the steady state regime
• This means:
  • We need to have the high frequency attenuation in the frequency range of the Bode plot that we want to shape
  • We need to push the phase lag to lower frequencies as much as possible

Let's go back to our Bode Plot

# s = control.tf([1, 0], [1])
# G_s = 1/(0.2*s+1)
# R_s = 50/s

# fig, ax = plt.subplots(1, figsize=(10,7))

# control.bode_plot(G_s*R_s, dB=True, margins=True, wrap_phase=True, omega_limits=[0.1, 1000]);

• We would need to decrease the gain by about 18 dB to have a crossover frequency with a 48 degree phase margin
• Add a safety margin (e.g., drop the gain by 20 dB to add some safety)

• Let's calculate how to have a drop in gain of 20dB or 10 at high frequency:

$$ R(s) = \frac{\tau_z\cdot s +1}{\tau_p\cdot s +1} \Rightarrow \frac{\tau_z}{\tau_p} = 10 $$

or, the relative ratio between the zero and the pole is 10:

$$ \frac{\tau_z s+1}{10\tau_p s+1} $$

• We want the phase lag as low frequency as possible.
• We need the zero and poles as close to the imaginary axis as possible (or $\tau$ as large as possible)
• The larger $\tau$, the closer to the imaginary axis is the pole-zero pair, the less the lag compensator interfere with the original system, while still acting to improve our phase margin
• This is the same approach that we used for the Root Locus to design the Lag compensator

Rule of thumb: place the zero 50 times closer to the origin as the dominant poles

For our case, we have a pole at $s=5$, which means we would like a zero at $s=(1/50)*5$, or if we use the time-constant representation $0.2*50$:

$$ Lag(s) = \frac{10s+1}{100s+1} $$

And here is the final controller:

$$ R(s) = \frac{50}{s}\frac{10s+1}{100s+1} $$

s = control.tf([1, 0], [1])

# System G(s)
G_s = 1/(0.2*s+1)

# Partial Compensator P(s)
P_s = 50/s

# Lead Compensator Lead(s)
Lead_s = (0.088*s+1)/(0.022*s+1)

# Lag Compensator Lag(s)
Lag_s = (10*s+1)/(100*s+1)

# Lead Lag compensator
R_s = 50/s*Lead_s*Lag_s

# create the axis and figure
fig, ax = plt.subplots(1, figsize=(10,7))

# Blue, uncompensated
control.bode_plot(P_s*G_s, dB=True, margins=True, wrap_phase=True, omega_limits=[0.0001, 1000], color='b');

# Green, Lead compensated
control.bode_plot(P_s*G_s*Lead_s, dB=True, margins=True, wrap_phase=True, omega_limits=[0.0001, 1000], color='g');

# Red, Lag compensated
control.bode_plot(P_s*G_s*Lag_s, dB=True, margins=True, wrap_phase=True, omega_limits=[0.0001, 1000], color='r');

• Compare the phase maring of both the Lead Compensated, and the Lag Compensated
• At low frequency the DC gain has not changed for any system
• With the Lag compensator we moved the cross-over frequency to lower frequency: we slowed down the system

We can see this plotting the step response

t_o, yout_o = control.step_response(control.feedback(P_s*G_s, 1), T=5)
t_lead, yout_lead = control.step_response(control.feedback(P_s*G_s*Lead_s, 1), T=5)
t_lag, yout_lag = control.step_response(control.feedback(P_s*G_s*Lag_s, 1), T=5)

fig, ax = plt.subplots(1, figsize=(10,7))

plt.plot(t_o, yout_o, color='b', label='Uncompensated');
plt.plot(t_lead, yout_lead, color='g', label='Lead compensated');
plt.plot(t_lag, yout_lag, color='r', label='Lag compensated');

plt.grid();
plt.legend();
plt.yticks(np.arange(0, 2, 0.1));

• The original system is less stable
• The Lead compensated is very fast
• The Lag compensated is slower

Note:

• A slower system does not react to high frequency noise as much, and this tends to be better
• If we do not need to track fast signals, a slower system can be better

Final comments

• This type of lead/lag compensators is designed in the frequency domain by determining $a$ from the amount of phase needed to satisfy the phase margin requirements, and determing $\tau$ to place the added phase at the new gain-crossover frequency.
• The lead compensator increases the gain of the system at high frequencies (the amount of this gain is equal to $a$). This can increase the crossover frequency, which will help to decrease the rise time and settling time of the system (but may amplify high frequency noise).
• A lead-lag compensator combines the effects of a lead compensator with those of a lag compensator. The result is a system with improved transient response, stability, and steady-state error.
• To implement a lead-lag compensator, first design the lead compensator to achieve the desired transient response and stability, and then design a lag compensator to improve the steady-state response of the lead-compensated system.