The SONAR equations

The “sonar equation” is a systematic way of estimating the expected signal-to-noise ratios for sonar (SOund Navigation And Ranging) systems. - The signal-to-noise ratio determines whether or not a sonar will be able to detect a signal in the presence of background noise in the ocean. - It takes into account the source level, sound spreading, sound absorption, reflection losses, ambient noise, and receiver characteristics. - The sonar equation is used to estimate the expected signal-to-noise ratios for all types of sonar systems. - Slightly different versions of the sonar equation are used for active (echo-ranging) and passive sonar systems.

Fundamental equations through which we can measure the performance of an acoustic system (a SONAR).

A sonar system can be influenced by a number of factors: - environmental conditions (ambient noise, acoustic loss, etc.) - how the sonar system is built (geometry, frequency, array length, etc.)

The combination of these aspects give us the overall performance of a specific system in a specific environment

For ex. - Bathymetric survey: the right sonar depends on the expected environment when I need to measure the bathymetry in the area of interest

What this means is that the datasheet is usually not enough to characterise the operational performance of the sonar

Sonar equations are relatively simple equations that express an intensity balance (in dB)
Through the SONAR equations we obtain the Signal-to-Noise (SNR) at the receiver
And hence the maximum range of the SONAR

Note: - acoustic intensity depends on frequency, but we will see that in the sonar equations frequency is not explicit - what this means is that applying the same equations at different frequencies we obtain different results

The same system can have different operational performance in space and time because space and time change the environment
Changing the source-receiver geometry based on the operational environmental characteristics we can optimise the SONAR performance (we operate the system better)
- If our sonar is deployed on robots that can move through the water column this can make a big impact

Passive SONAR equation

The SONAR is a receiver that listens for sound
A source is emitting a signal with intensity \(SL\) (Source Level)
- Tonals (monofrequency components)
  - Propulsion machinery (main motors, reductions, etc.)
  - Auxiliary machinery (pumps, generators, etc)
  - etc.
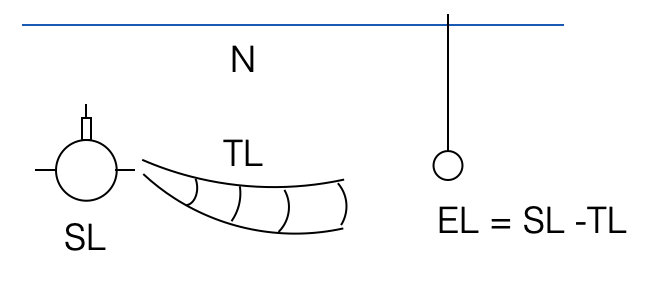
  \(SL\): Level of acoustic intensity 1m from the source
- Broadband noise
  - Cavitation at or near the propeller
  - Radiated flow noise
  - etc
  \(SL = SSL + 10\log B\)
  
  where:
  - \(SSL\) is the pressure spectrum level 1m from the source
  - \(B\) is the bandwidth of the system in Hz (if SSL is not contant over B, it needs to be split in smaller bands)
All the Ambient Noise present has an intensity \(N\) (e.g., marine traffic, etc.)
The receiver receives a signal (echo level) with intensity

\[ EL = SL - TL \]

Transmission Loss (TL) includes intrinsic attenuation, geometric attenuation, interference (which are also due to the variation of the sound speed in the water column)
- TL is due to the environmental effects (except for the noise)
- There might be one loss that is predominant, for ex. at high freq. TL mostly due to intrinsic attenuation, at low frequency (and deep water) is geometric attenuation
The equation depends on the frequency so is valid if all the quantities have the same frequencies
- Note that interference which depends on the phase is strongly dependent on the frequency and this has a direct effect on the TL

The Signal-to-Noise ratio in dB:

\[ SNR = (SL - TL) - N \]

Detection Threshold and Signal Eccess

We are interested in listening to some signal (EL) which is due to the sound emitted by the source less than what is loss due to propagation.
Given that there is also Ambient noise, when can I detect the signal from the Ambient noise?
We define a Detection Threshold (DT) (typically DT=0, SNR > 0 dB)
- Choose the right DT value is complex
- Trade off between probability of detecting something but also having as little false alarms as possible
- Depends on the application
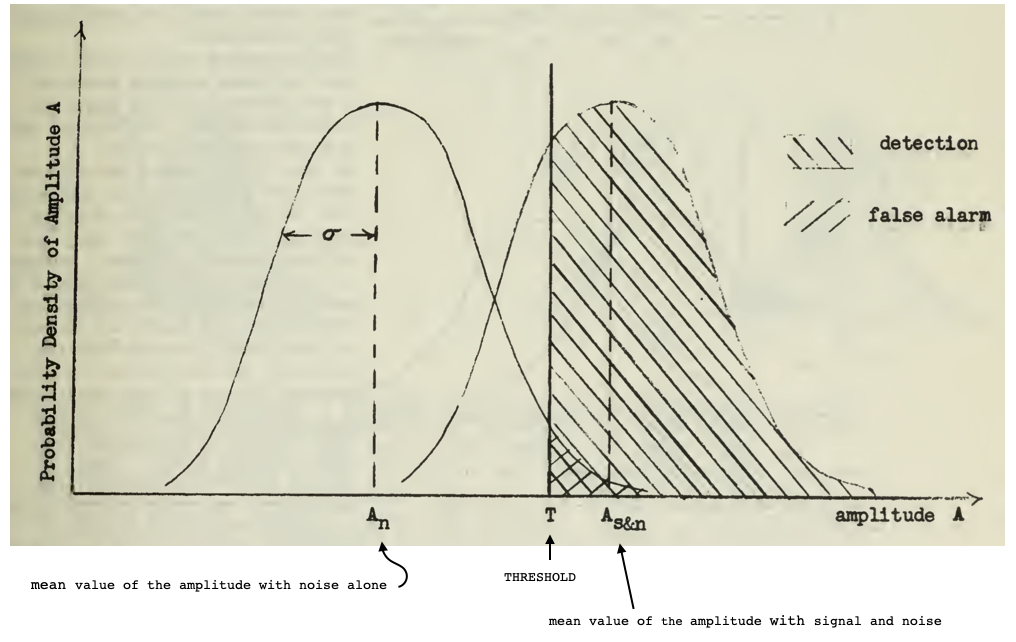
The detection process consists of designating a threshold which, when exceed, causes a detection to be recorded.
If the signal is much stronger than the noise, it is clear that a threshold can be defined that will allow valid signals to be recorded while ignoring the noise.
However, when the signal and noise are of comparable size, any threshold that will catch a reasonable number of valid signals will also record “detections” when a valid signal is absent.

Figure: Adapted from An introduction to the sonar equations with applications, 1976, pag. 81

We call Signal Eccess (SE)

\[ SE = SNR - DT \]

If \(SE>0\) we “see” the signal, otherwise we do not see it.

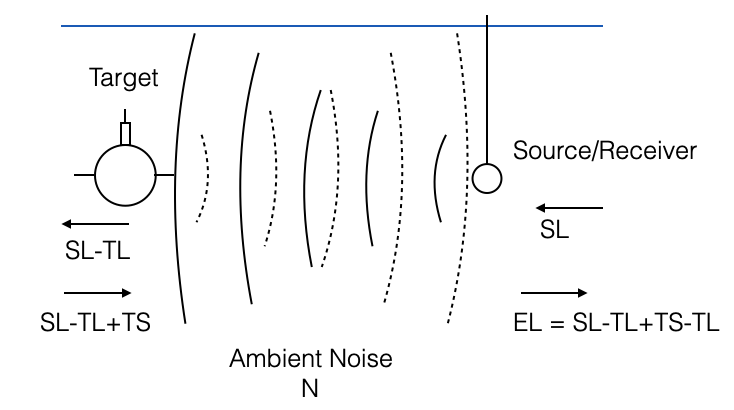
Active monostatic SONAR equation

Monostatic: source and receiver are collocated
- Might be the same transducer or different transducers
Active SONAR:
- The system produces sound
- We have a source with a specific souce (\(SL\))
If souce and receiver are collocated and given that the source has transmitted a signal and I expect to receive a signal
- the signal must be backscatter from something
- the signal must come back to the receiver (which is collocated with the source)
For this reason we need to have a “Target” in the area

Target

Terminology comes from military applications (active sonars developed to hunt for submarines)
For us, target is anything we would like to insonify
The backscatter signal depends on the target
- With respect to the wavelength of the signal
- The intensity of the signal reflected by the target is called Target Strength \(TS\)
- The Target Strength is typically negative!
  - Provides information on how much signal is lost through scattering in every direction but the backscatting one
- The Target Strength of the target depends on the target shape and where the signal insonifies that specific shape (e.g. submarine)

Ambient Noise

We have the usual Ambient Noise (\(N\))
We also have a different type of noise, called Reverberation (\(RL\))
- Depends on the reflections off the boundaries (sea surface, seabed) and off anything that is present in the water column (e.g., schools of fish, etc.)
- We call reverberation the scatting coming from anything that is present in the environment except for the target.
- It can arrive from all directions
- Reverberation would not be present if sonar did not transmit

Signal-To-Noise Ratio

\[ SNR = EL - (N+RL) \]

And the Signal Eccess is

\[ SE = SNR - DT \]

A further comment on the Signal-to-Noise Ratio:

\(N+RL\) means that the reverberation level is multiplied by the noise level (in dB we sum them up). This is not true, because the two signal physically sum up
\(N+RL\) is not a sum even when we are in dB.
One of the two terms will be dominant and we reduce the equation to only use that term

This means:

Received signal \(s\): \[ S = 10\log|s| \]
Ambient noise \(n\): \[ N = 10\log|n| \]
Reverberation level \(rl\): \[ RL = 10\log|rl| \]
Signal to noise ratio \[ snr = \frac{|s|}{|n+rl|} \Rightarrow SNR = 10\log\frac{|s|}{|n+rl|} \Rightarrow S-10\log(|n+rl|) \]

Let’s analyse \(10\log(|n+rl|)\).

\[ 10\log(|n+rl|) \le 10\log(|n|+|rl|) \]

Let’s consider now the case where the reverberation level is less than the noise (the other case would be the same):

\[ |rl| \le |n| \Rightarrow |rl| = k|n|\;\; k \in [0,1] \]

This means that

\[ 10\log(|n|+|rl|) = 10\log((k+1)|n|) = N + 10\log(k+1) \;\; k \in [0,1] \]

if \(k=0\) (no reverberation): we have the usual noise only equation
if \(k=1\) (reverberation is as loud as the noise) and our expression becomes:

\[ N + 10\log(k+1) = N+10\log2 = N + 3 dB \]

This means that \[10\log(|n|+|rl|) \in [N, N+3]\]

Note that if \(|rl| > |n|\) we can repeat the same reasoning with noise as a fraction of the reverberation level and we would obtain:

\[10\log(|n|+|rl|) \in [RL, RL+3]\]

With respect to the larger between \(N\) and \(RL\), the intensity in dB of their sum, can only be 3dB more than the maximum between \(N\) and \(RL\) (which is when they both have the same value). Otherwise is less than 3dB.

Three dB is the usual approximation level that we use.

In practise, in most cases we can neglect one of the two terms. In the worst case scenario where the two levels are comparable we add 3dB.

We talk about: - Noise limited environments when the ambient noise is prevalent \(|rl| \le |n|\). The SNR only depends on the ambient noise

Reverberation limited environments when the reverberation level is prevalent \(|n| \le |rl|\). The SNR only depends on the reverberation Level

For example, consider the case where the noise and the reverberation level have the same intensity level: - \(10\log(N)=60dB\) - \(10\log(RL)=60dB\)

In natural scale we need to sum them and they are equal:

\[ N_{tot} = N+RL=2N \rightarrow 10\log2N = 10\log N + 10\log2 \approx 60 + 3 = 10\log(|n|+|rl|) \]

If, for example, \(N>RL\), \(N+RL\) will be less than \(2N\), which means that the difference will be less than 3dB

In the sonar equation \(N+RL\) = 63 dB (not 120)

Often our systems are able to measure differences of 3dB..
This is a confusing way of representing \(N\) and \(RL\) in the sonar equation but it is standard terminology.

If we had: \(N=60dB\) and \(RL=40dB\)

A difference of \(20dB\) corresponds to two orders of magnitude, so \(RL\) is negligible and in the sonar equation \(N+RL\)=60dB

We are implicity assuming Reciprocity - Waves are linear - Environment does not change in time (it can change in space) - Propagation loss in both directions are the same

Active bistatic SONAR equation

Active: there is a source of sound that transmits a signal
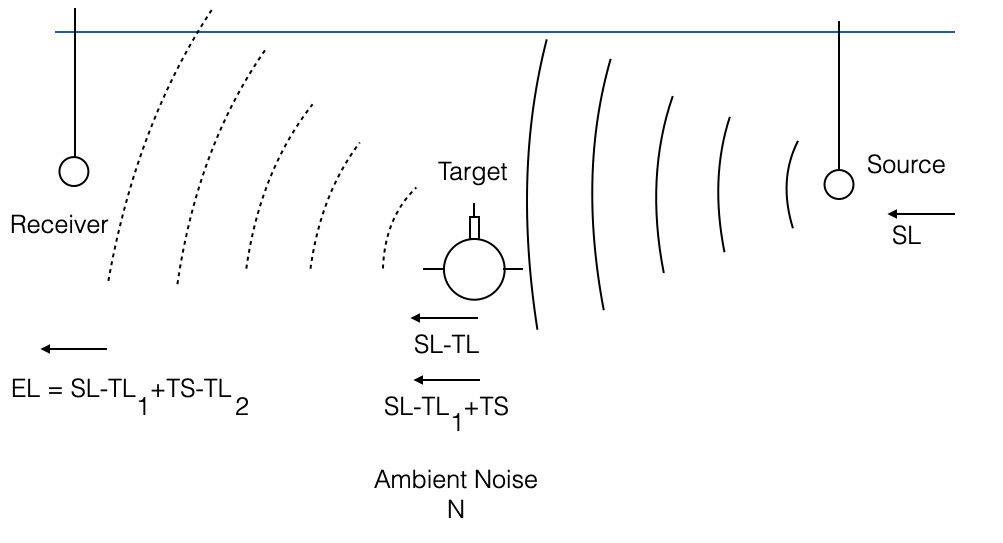
Bistatic: receiver is in a geomtric location that is different from the transmitter
Received signal: scattering from the target with some angle (there will be a scattering angle from the target to the receiver)
The receiver would receive also scattering from other surfaces or volumes present in the environment

\[ EL = SL - TL_1 - TL_2 + TS \]

\[ SNR = S - (N+RL) \]

\[ SE = SNR - DT \]

Determining SONAR performance

How can these equations determine the range of the system?
Let’s focus on a passive sonar (which is easier)
DT is fixed (chosen by the operator) and is the only parameter of the SONAR
SL is unknown

Let’s consider a specific example:

Deep waters, sound speed is a Munk profile, etc. (this means that we are in a specific area)
We want to listen to sound emitted by a marine mammal
- \(SL=180\)dB (this might come from previous experiments).
- \(DT=20\)dB

Ambient noise: depends on the frequency (e.g., 2-5kHz). Assuming that the sea state is 2 (no experiment if sea state is too rough), so \(N\approx60dB\).

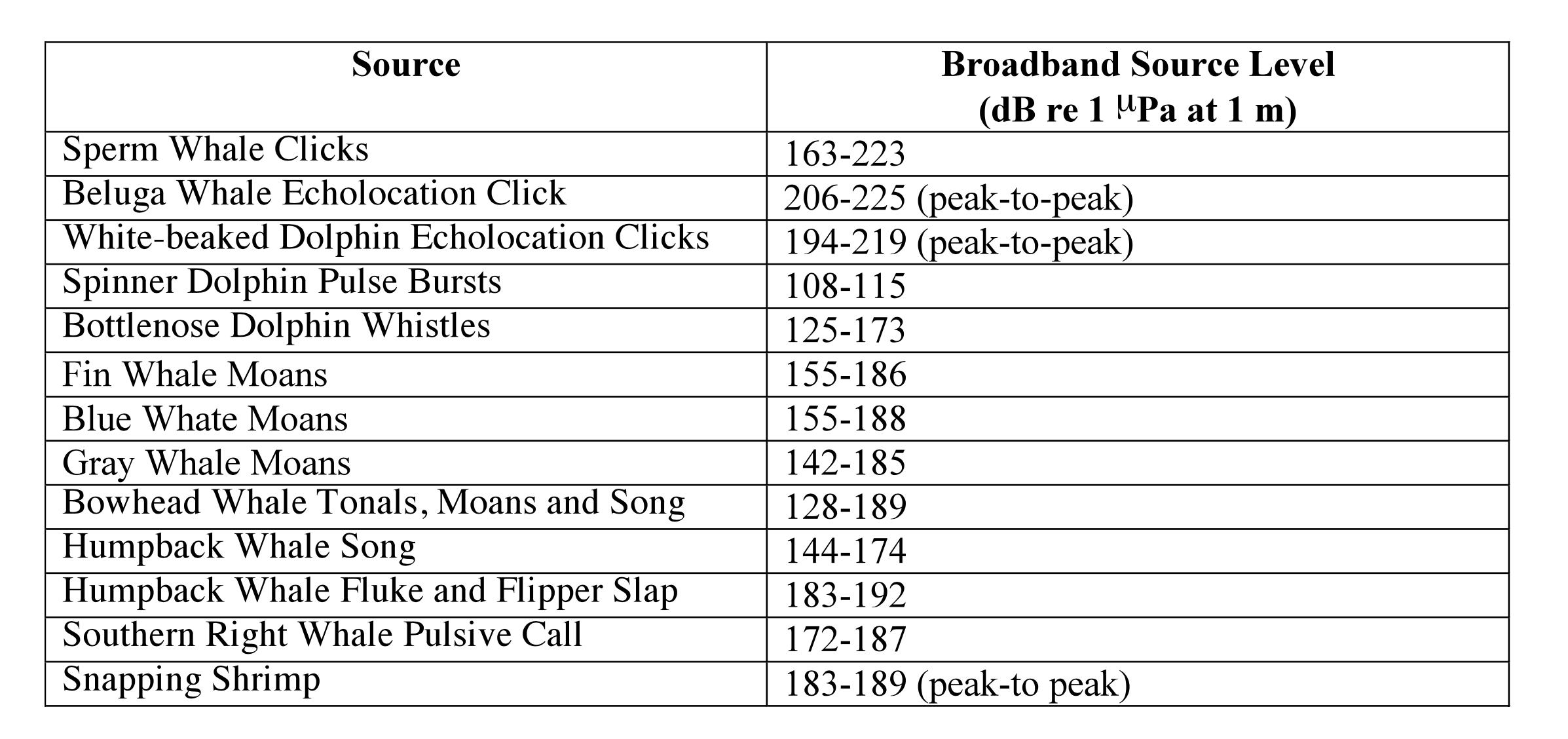
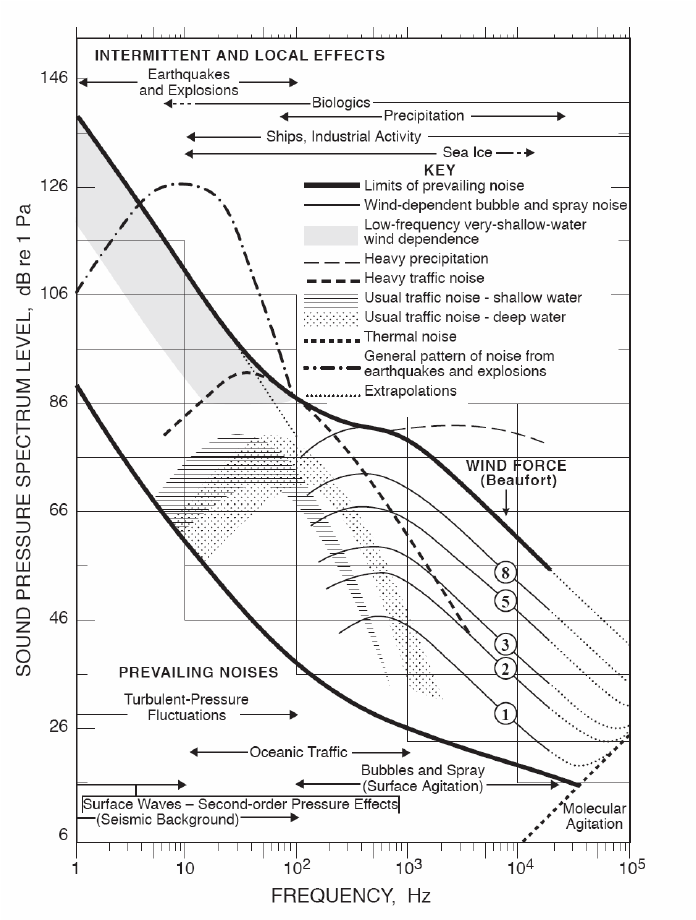
14.Composite-of-ambient-noise-spectra-from-Wenz-1962.png

What is the maximum distance of the whale from the receiver at which the receiver can record the whale?
Assuming that we can neglect interference in this environment.
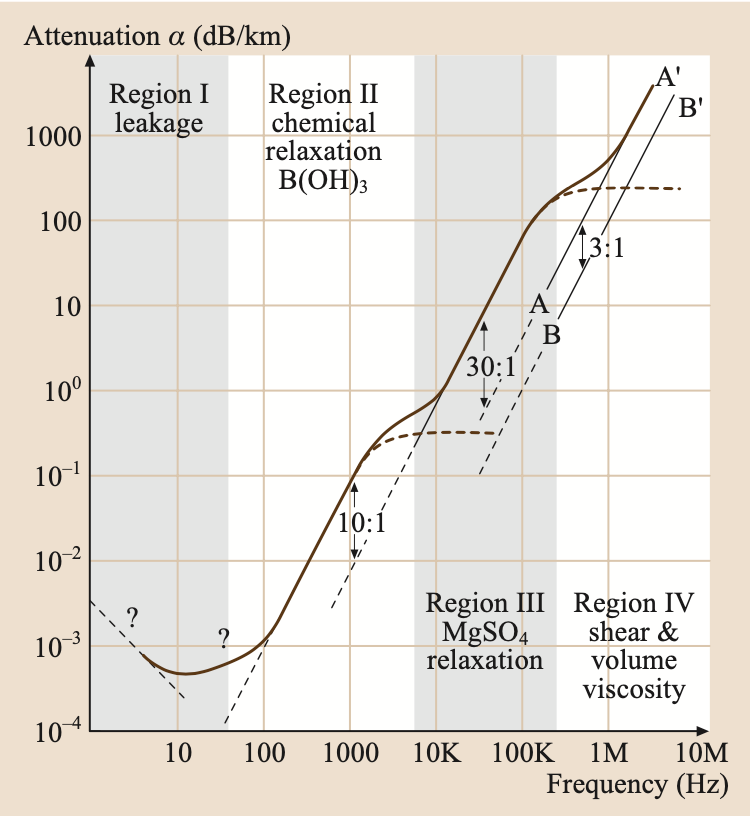
This means that for the TL we can consider the intrinsic attenuation and the geometric attenuation. We are between 2-5kHz and if we look at the attenuation vs frequency:

At \(5kHz\), intrinsic attenuation is \(\alpha \approx 1 db/km\).

The geometric attenuation is \(GA \approx 20\log R\) where \(R\) is in metres. - If \(R=1000m\), \(GA=60dB\)

In this scenario, the main attenuation is geometric. This means:

\[ TL = 20\log R \]

I have everything I need to use the SONAR equations:

\(EL = SL - TL = 180 - 20\log R\)
\(SNR = SL - TL - N = 180 - 20\log R - 60 = 120 - 20\log R\)
\(SE =SNR - DT= 120 -20\log R - 20 = 100 -20\log R\)

To have detection, we need \(SE \ge0\) and the maximum range where \(SE = 0\), which means:

\[ 20\log_{10} R = 100 \Rightarrow R = 10^5 m = 100 km \]

At this point we could fine tune it using the intrinsic attenuation. With a 100km propagation a \(5 dB/km\) (\(5e^{-3} dB/m\)) loss becomes important.

\[ TL = 20\log R + 5e^{-3}R \]

The equation becomes:

\[ 20\log_{10} R + 5e^{-3}R = 100 \]

This is a transcendental equation. We can solve it trying a few values to get a maximum range of about 5km.

I can detect marine mammals up to 5km. I can change the DT to extend the maximum range, but I would increase the number of false alarms as well.

import numpy as np

for R in range(1000, 10000, 1000):
    SE = 20*np.log10(R) + 5e-3*R - 100
    if abs(SE) < 5: 
        print(f'SE:{SE}, max range: {R}')
        break

SE:-1.020599913279625, max range: 5000